
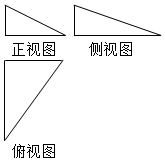
 己知三棱锥的三视图如图所示,其主视图、侧视图、俯视图的面积分别为1,$\frac{3}{2}$,3,则该三棱锥的外接球体积为( )
己知三棱锥的三视图如图所示,其主视图、侧视图、俯视图的面积分别为1,$\frac{3}{2}$,3,则该三棱锥的外接球体积为( )| A. | $\frac{28\sqrt{14}}{3}$π | B. | $\frac{56\sqrt{14}}{3}$π | C. | $\frac{7\sqrt{14}}{3}$π | D. | $\frac{7\sqrt{14}}{6}$ |
分析 几何体是一个三棱锥,一条侧棱与底面垂直,底面是一个直角三角形,根据正视图、侧视图、俯视图面积分别是1,$\frac{3}{2}$,3.求出三条边的长度,这个三棱锥的外接球也是以这个三棱锥三条侧棱为棱的长方体的外接球,做出长方体的对角线,求出三棱锥的外接球体积.
解答 解:由题意知几何体是一个三棱锥,一条侧棱与底面垂直,底面是一个直角三角形,
∵正视图、侧视图、俯视图面积分别是1,$\frac{3}{2}$,3,
设出三条互相垂直的棱长是x,y,z,
有xz=2,yz=3,xy=6,
∴x=2,y=3,z=1
这个三棱锥的外接球也是以这个三棱锥三条侧棱为棱的长方体的外接球,
长方体的对角线长是$\sqrt{4+9+1}$=$\sqrt{14}$,三棱锥的外接球的半径为$\frac{\sqrt{14}}{2}$,
∴三棱锥的外接球体积是$\frac{4}{3}π•(\frac{\sqrt{14}}{2})^{3}$=$\frac{7\sqrt{14}}{3}$π,
故选:C.
点评 本题考查球和几何体之间的关系,本题解题的关键是根据三条侧棱两两垂直的关系得到由这三条侧棱构成的长方体,从而得到三棱锥的外接球体积.


科目:高中数学 来源: 题型:解答题
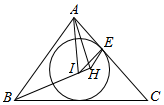 如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.
如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
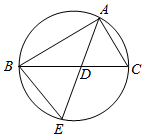 如图,△ABC的角平分线AD的延长线交它的外接圆于点E.
如图,△ABC的角平分线AD的延长线交它的外接圆于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
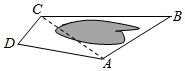 如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.
如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.| A. | 7 | B. | 8 | C. | 9 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.
某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com