
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$.(1)求椭圆C的方程;
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$.(1)求椭圆C的方程;分析 (1)利用椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$,建立方程,求出a,b,即可求椭圆C的方程;
(2)①求出B的坐标,即可证明PB平分线段CD;
②表示出△PBC面积,可得最大值,并求此时C点坐标.
解答 (1)解:∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$,
∴2c=2$\sqrt{3}$,$\frac{1}{{a}^{2}}$+$\frac{\frac{3}{4}}{{b}^{2}}$=1,
∴c=$\sqrt{3}$,a=2,b=1,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1;
(2)①证明:设C(x1,y1),则切线PC的方程为$\frac{{x}_{1}}{4}x+{y}_{1}y$=1,
令x=-2,可得y=$\frac{1}{{y}_{1}}$+$\frac{{x}_{1}}{2{y}_{1}}$,即P(-2,$\frac{1}{{y}_{1}}$+$\frac{{x}_{1}}{2{y}_{1}}$),
∵B(2,0),∴直线PB的方程为y-0=-$\frac{1}{4}$($\frac{1}{{y}_{1}}$+$\frac{{x}_{1}}{2{y}_{1}}$)(x-2),
令x=x1,则y=$\frac{1}{2}$y1,
∴PB平分线段CD;
②解:由①切线PC的方程为$\frac{{x}_{1}}{4}x+{y}_{1}y$=1,令y=0,可得x=$\frac{4}{{x}_{1}}$,
∴△PBC面积=$\frac{1}{2}•$($\frac{4}{{x}_{1}}$-2)•|$\frac{1}{{y}_{1}}$+$\frac{{x}_{1}}{2{y}_{1}}$-y1|=|$\frac{4-{{x}_{1}}^{2}}{4{y}_{1}}$|=|y1|≤1
∴△PBC面积的最大值为1,此时C点坐标为(0,1)或(0,-1).
点评 本题考查椭圆的方程与性质,考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,有难度.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
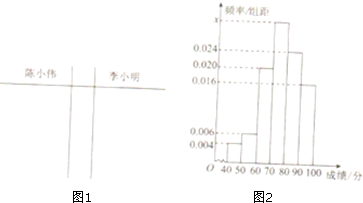 某大学在自主招生面试环节中.七位评委老师为陈小伟,李小明打出了分数,要求统计组、复核组依次打出的分数进行统计,复核组拿到了有两处污染的成绩单(成绩为40-100的整数)如表
某大学在自主招生面试环节中.七位评委老师为陈小伟,李小明打出了分数,要求统计组、复核组依次打出的分数进行统计,复核组拿到了有两处污染的成绩单(成绩为40-100的整数)如表| 考生姓名 | 评委01 | 评委02 | 评委03 | 评委04 | 评委05 | 评委06 | 评委07 |
| 陈小伟 | 99 | 70 | 85 | 84 | 8■ | 85 | 81 |
| 李小明 | 79 | 9■ | 84 | 84 | 86 | 84 | 87 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
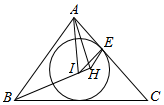 如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.
如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
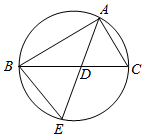 如图,△ABC的角平分线AD的延长线交它的外接圆于点E.
如图,△ABC的角平分线AD的延长线交它的外接圆于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com