
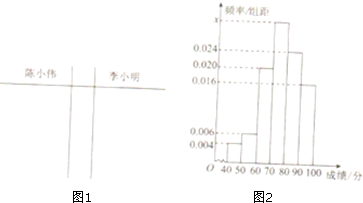
 某大学在自主招生面试环节中.七位评委老师为陈小伟,李小明打出了分数,要求统计组、复核组依次打出的分数进行统计,复核组拿到了有两处污染的成绩单(成绩为40-100的整数)如表
某大学在自主招生面试环节中.七位评委老师为陈小伟,李小明打出了分数,要求统计组、复核组依次打出的分数进行统计,复核组拿到了有两处污染的成绩单(成绩为40-100的整数)如表| 考生姓名 | 评委01 | 评委02 | 评委03 | 评委04 | 评委05 | 评委06 | 评委07 |
| 陈小伟 | 99 | 70 | 85 | 84 | 8■ | 85 | 81 |
| 李小明 | 79 | 9■ | 84 | 84 | 86 | 84 | 87 |
分析 (1)画出茎叶图,计算平均数以及方差,从而判断李小明的成绩稳定;
(2)设评委05给学生陈小伟打出的分数为:80+m,分别求出其平均分,作差判断即可;
(3)(i)求出第四小组的频率,根据第四小组(即[70,80)内)的频数是15,求出n的值即可,(ii)设出中位数,得到估计值即可.
解答 解:(1)两位同学成绩的茎叶图如图所示: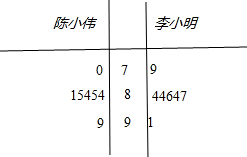 ,
,
$\overline{{x}_{陈}}$=$\frac{70+84+85+84+85+81+99}{7}$=84,
${\overline{x}}_{李}$=$\frac{79+84+84+86+84+87+91}{7}$=85,
故${s}_{{陈}_{\;}}$=$\sqrt{\frac{{(70-84)}^{2}+…{+(81-84)}^{2}{+(99-84)}^{2}}{7}}$=$\sqrt{\frac{432}{7}}$,
同理可得:s李=$\sqrt{\frac{80}{7}}$,s李<s陈,
故考生李小明的成绩较为稳定;
(2)设评委05给学生陈小伟打出的分数为:80+m,
(m∈{0,1,2,3,4,5,6,7,8,9}),
将考生成绩去掉一个最高分和一个最低分,
陈小伟的成绩数据分别为:85,84,80+m,85,81,
${\overline{x}}_{陈}$=$\frac{85+84+80+m+85+81}{5}$,
${\overline{x}}_{李}$=$\frac{84+84+86+84+87}{5}$,且${\overline{x}}_{陈}$-${\overline{x}}_{李}$=$\frac{m-10}{5}$,
又m∈{0,1,2,3,4,5,6,7,8,9},
∴${\overline{x}}_{陈}$-${\overline{x}}_{李}$<0,
故李小明同学的平均水平较高;
(3)(i)∵10×(0.004+0.006+0.016+0.020+0.024+x)=1,
解得:x=0.030,
第四小组的频率为:0.030×10=0.30,
又第四小组(即[70,80)内)的频数是15,
故$\frac{15}{n}$=0.30,解得:n=50;
(ii)由频率分布直方图可知[70,80)这一组对应的小长方形最高,估计众数是75,设中位数是(70+x),
则0.04+0.06+0.20+0.03x=0.5,解得:x≈6.67,
估计中位数是76.67,
45×0.04+55×0.06+65×0.20+75×0.30+85×0.24+95×0.16=76.20,
估计平均数是76.20.
点评 本题考查了平均数、标准差的计算,考查茎叶图、直方图的应用,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln3 | B. | 2ln2 | C. | 2ln3 | D. | ln6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-2,4) | B. | (3,2,-4) | C. | (3,2,4) | D. | (-3,-2,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$.(1)求椭圆C的方程;
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$.(1)求椭圆C的方程;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com