
| A. | ln3 | B. | 2ln2 | C. | 2ln3 | D. | ln6 |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,求出最大值和最小值,结合积分的公式进行求解即可.
解答 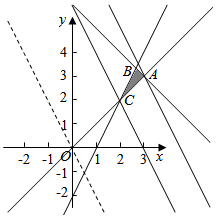 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
由z=2x+y得y=-2x+z
平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点A时,直线y=-2x+z的截距最大,
此时z最大.
由$\left\{\begin{array}{l}{y=x}\\{x+y-6=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,j即A(3,3),
此时z=2x+y得z=2×3+3=9.即n=9,
当直线y=-2x+z经过点C时,直线y=-2x+z的截距最小,
此时z最小.
由$\left\{\begin{array}{l}{y=x}\\{2x-y-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,即C(2,2),
代入目标函数z=2x+y得z=2×2+2=6.
即m=6,
则$\int_m^n$($\frac{1}{x}$+$\frac{ln2}{3}$)dx=${∫}_{6}^{9}$($\frac{1}{x}$+$\frac{ln2}{3}$)dx=(lnx+$\frac{ln2}{3}$x)|${\;}_{6}^{9}$=ln9+9×$\frac{ln2}{3}$-ln6-$\frac{ln2}{3}$×6
=ln9+3ln2-ln6-2ln2=ln9+ln8-ln6-ln4=ln$\frac{8×9}{6×4}$=ln3,
故选:A
点评 本题主要考查线性规划和积分的计算,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
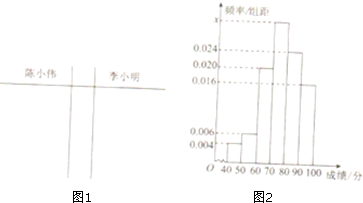 某大学在自主招生面试环节中.七位评委老师为陈小伟,李小明打出了分数,要求统计组、复核组依次打出的分数进行统计,复核组拿到了有两处污染的成绩单(成绩为40-100的整数)如表
某大学在自主招生面试环节中.七位评委老师为陈小伟,李小明打出了分数,要求统计组、复核组依次打出的分数进行统计,复核组拿到了有两处污染的成绩单(成绩为40-100的整数)如表| 考生姓名 | 评委01 | 评委02 | 评委03 | 评委04 | 评委05 | 评委06 | 评委07 |
| 陈小伟 | 99 | 70 | 85 | 84 | 8■ | 85 | 81 |
| 李小明 | 79 | 9■ | 84 | 84 | 86 | 84 | 87 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,0} | B. | {-2} | C. | {-2,3} | D. | {0,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,D是棱AA1上的任一点,M,N分别为AB,BC1的中点.
如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,D是棱AA1上的任一点,M,N分别为AB,BC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
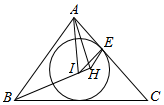 如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.
如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com