
分析 利用三角函数的降幂公式化简$\frac{{{{sin}^2}{a_3}-{{sin}^2}{a_7}}}{{sin({a_3}+{a_7})}}$=-1,得出$\frac{cos{2a}_{7}-cos{2a}_{3}}{2}$=-sin(a3+a7),再利用和差化积公式得出sin(a7-a3)=1,求出公差d的值,写出通项公式an,令an≤0,即可求得n的值.
解答 解:∵{an}为等差数列,且$\frac{{{{sin}^2}{a_3}-{{sin}^2}{a_7}}}{{sin({a_3}+{a_7})}}$=-1,
∴$\frac{\frac{1-cos{2a}_{3}}{2}-\frac{1-cos{2a}_{7}}{2}}{sin{(a}_{3}{+a}_{7})}$=-1,
∴$\frac{cos{2a}_{7}-cos{2a}_{3}}{2}$=-sin(a3+a7),
由和差化积公式得:$\frac{1}{2}$×(-2)sin(a7+a3)•sin(a7-a3)=-sin(a3+a7),
又sin(a3+a7)≠0,
∴sin(a7-a3)=1,
∴4d=2kπ+$\frac{π}{2}$∈(0,4);
取k=0,得4d=$\frac{π}{2}$,解得d=$\frac{π}{8}$;
又∵a1∈(-$\frac{5π}{4}$,-$\frac{9π}{8}$),∴an=a1+$\frac{π}{8}$(n-1),
∴an∈(-$\frac{11π}{8}$+$\frac{nπ}{8}$,-$\frac{10π}{8}$+$\frac{nπ}{8}$);
令an≤0,得-$\frac{10π}{8}$+$\frac{nπ}{8}$≤0,
解得n≤10;
∴n=10时,数列{an}的前n项和Sn取得最小值.
故答案为:10.
点评 本题考查了数列与三角函数的综合应用问题,利用三角函数的降幂公式与和差化积公式求得sin(a7-a3)=1是关键,也是难点,是综合性题目.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | log${\;}_{\frac{1}{2}}$17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
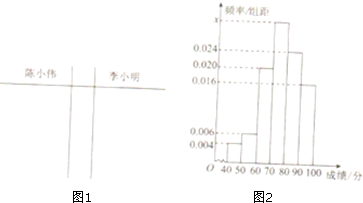 某大学在自主招生面试环节中.七位评委老师为陈小伟,李小明打出了分数,要求统计组、复核组依次打出的分数进行统计,复核组拿到了有两处污染的成绩单(成绩为40-100的整数)如表
某大学在自主招生面试环节中.七位评委老师为陈小伟,李小明打出了分数,要求统计组、复核组依次打出的分数进行统计,复核组拿到了有两处污染的成绩单(成绩为40-100的整数)如表| 考生姓名 | 评委01 | 评委02 | 评委03 | 评委04 | 评委05 | 评委06 | 评委07 |
| 陈小伟 | 99 | 70 | 85 | 84 | 8■ | 85 | 81 |
| 李小明 | 79 | 9■ | 84 | 84 | 86 | 84 | 87 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,0} | B. | {-2} | C. | {-2,3} | D. | {0,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com