Question

10．如图，已知三棱柱ABC-A′B′C′的所有棱长都是2，且∠A′AB=∠A′AC=60°．
（1）求证：点A′在底面ABC内的射影在∠BAC的平分线上；
（2）求棱柱ABC-A′B′C′的体积．

Answer 1

分析 （1）设A′在底面ABC上的射影为O，连接A′O，过A′分别作A′D⊥AB于D，A′E⊥AC于E，连接OD，OA，OE．通过证明AC⊥平面A′OE得出AC⊥OE，同理得出OD⊥AB，利用三角形全等得出OD=OE，结论得证；
（2）利用勾股定理计算A′O，代入棱柱的体积公式计算．

解答 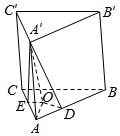证明：（1）设A′在底面ABC上的射影为O，连接A′O，过A′分别作A′D⊥AB于D，A′E⊥AC于E，连接OD，OA，OE．
∵∠A′AB=A′AC=60°，∠A′DA=∠A′EA=90°，AA′=2，
∴AD=AE=1，A′D=A′E=$\sqrt{3}$．
∵A′O⊥平面ABC，OD?平面ABC，OE?平面ABC，
∴A′O⊥OD，A′O⊥OE，又A′O为公共边，
∴△A′OD≌△A′OE，∴OD=OE．
又∵AC⊥A′E，AC⊥A′O，A′O∩A′E=A′，
∴AC⊥平面A′OE，∵OE?平面A′OE，
∴AC⊥OE．
同理可得OD⊥AB．
∴O到AB，AC的距离相等．
∴O在∠BAC的角平分线上．
（2）由（1）知AD=1，∠OAD=30°，OD⊥AB，
∴OA=$\frac{2\sqrt{3}}{3}$，∴A′O=$\sqrt{AA{′}^{2}-A{O}^{2}}$=$\frac{2\sqrt{6}}{3}$．
∴V_{ABC-A′B′C′}=S_△ABC•A′O=$\frac{1}{2}×2×2×sin60°×\frac{2\sqrt{6}}{3}$=2$\sqrt{2}$．

点评 本题考查了棱柱的结构特征，线面垂直的判定，棱柱的体积计算，属于中档题．