
| A. | 若|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,则$\overrightarrow{a}$>$\overrightarrow{b}$ | B. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若$\overrightarrow{a}$=$\overrightarrow{b}$,则$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | 若$\overrightarrow{a}$≠$\overrightarrow{b}$,则$\overrightarrow{a}$与$\overrightarrow{b}$不是共线向量 |
分析 根据平面向量的基本概念,对选项中的命题进行分析、判断即可.
解答 解:向量的模长能比较大小,但向量不能比较大小,故选项A错误;
当|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,方向不同时,$\overrightarrow{a}$=$\overrightarrow{b}$不成立,所以B错误;
当$\overrightarrow{a}$=$\overrightarrow{b}$时,$\overrightarrow{a}$与$\overrightarrow{b}$方向相同,模长相等,所以$\overrightarrow{a}$∥$\overrightarrow{b}$,C正确;
当$\overrightarrow{a}$≠$\overrightarrow{b}$时,$\overrightarrow{a}$与$\overrightarrow{b}$也可能是共线向量,所以D错误.
故选:C.
点评 本题考查了平面向量的基本概念与应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱柱ABC-A′B′C′的所有棱长都是2,且∠A′AB=∠A′AC=60°.
如图,已知三棱柱ABC-A′B′C′的所有棱长都是2,且∠A′AB=∠A′AC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示的正数数阵中,第一横行是公差为d的等差数列,各列均是公比为q等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,则下列结论中不正确的是( )
如图所示的正数数阵中,第一横行是公差为d的等差数列,各列均是公比为q等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,则下列结论中不正确的是( )| A. | d+2q=a1,2 | B. | a2,1+a2,3+a2,5+…+a2,21=$\frac{441}{2}$ | ||
| C. | 每一横行都是等差数列 | D. | ai,j=(2j-1)+21-i(i,j均为正整数) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
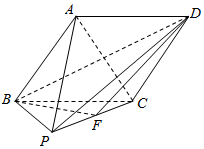 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
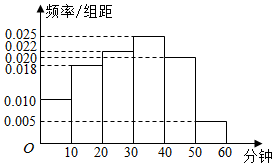 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 60 | 30 | 90 |
| 女 | 90 | 20 | 110 |
| 合计 | 150 | 50 | 200 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com