
| A. | [kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z | B. | [kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z | ||
| C. | [kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$],k∈Z | D. | [kπ+$\frac{3π}{8}$,kπ+$\frac{7π}{8}$],k∈Z |
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.
某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.
设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱柱ABC-A′B′C′的所有棱长都是2,且∠A′AB=∠A′AC=60°.
如图,已知三棱柱ABC-A′B′C′的所有棱长都是2,且∠A′AB=∠A′AC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
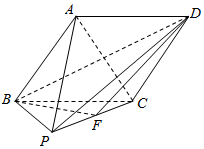 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,侧面PBC是边长为2的等边三角形,点E是PC的中点,且平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6个 | B. | 9个 | C. | 12个 | D. | 24个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com