
 如图,据气象部门预报,在距离某码头南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方 向移动,距风暴中心450km以内的地区都将受到影响,则该码头将受到热带风暴影响的时间为( )
如图,据气象部门预报,在距离某码头南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方 向移动,距风暴中心450km以内的地区都将受到影响,则该码头将受到热带风暴影响的时间为( )| A. | 14h | B. | 15h | C. | 16h? | D. | 17h |
分析 设风暴中心最初在A处,经th后到达B处.自B向x轴作垂线,垂足为C.若在点B处受到热带风暴的影响,则OB=450,求出t,即可得出结论.
解答 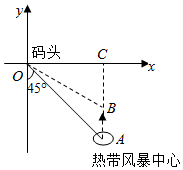 (本题满分为12分)
(本题满分为12分)
解:设风暴中心最初在A处,经th后到达B处.自B向x轴作垂线,垂足为C.
若在点B处受到热带风暴的影响,则OB=450,
即$\sqrt{O{C}^{2}+B{C}^{2}}$=450,…(2分)
即$\sqrt{(600cos45°)^{2}+(600sin45°-20t)^{2}}$=450,…(4分)
上式两边平方并化简、整理得4t2-120$\sqrt{2}$t+1575=0,…(6分)
解得t=$\frac{15(2\sqrt{2}-1)}{2}$或$\frac{15(2\sqrt{2}+1)}{2}$,…(9分)
又$\frac{15(2\sqrt{2}-1)}{2}$≈13.7,$\frac{15(2\sqrt{2}+1)}{2}$-$\frac{15(2\sqrt{2}-1)}{2}$=15,…(11分)
所以,经过约13.7后,该码头将受到热带风暴的影响,影响时间为15h.
故选:B.…(12分)
点评 本题主要考查了解三角形的实际应用.考查了学生解决实际问题的能力,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
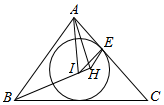 如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.
如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{1}{4}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
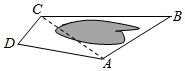 如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.
如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.| A. | 7 | B. | 8 | C. | 9 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com