
分析 (1)列方程组解出首项和公差,即可得出通项公式;
(2)利用裂项法求和.
解答 解:(1)设{an}公差为d,∵a3=5,S5=3S3-2.
∴$\left\{\begin{array}{l}{{a}_{1}+2d=5}\\{5{a}_{1}+10d=3(3{a}_{1}+3d)-2}\end{array}\right.$,解得a1=1,d=2.
∴an=2n-1.
(2)bn=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}-\frac{1}{2n+1}$),
∴Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}-\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{2}•$$\frac{2n}{2n+1}$=$\frac{n}{2n+1}$.
点评 本题考查了等差数列的性质,列项法数列求和,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{1}{4}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
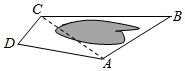 如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.
如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.| A. | 7 | B. | 8 | C. | 9 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
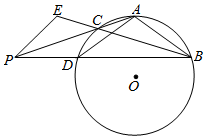 如图,A,B是⊙O上的两点,P为⊙O外一点,连结PA,PB分别交⊙O于点C,D,且AB=AD,连结BC并延长至E,使∠PEB=∠PAB.
如图,A,B是⊙O上的两点,P为⊙O外一点,连结PA,PB分别交⊙O于点C,D,且AB=AD,连结BC并延长至E,使∠PEB=∠PAB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.
设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com