
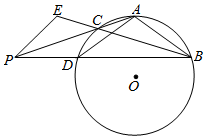
 如图,A,B是⊙O上的两点,P为⊙O外一点,连结PA,PB分别交⊙O于点C,D,且AB=AD,连结BC并延长至E,使∠PEB=∠PAB.
如图,A,B是⊙O上的两点,P为⊙O外一点,连结PA,PB分别交⊙O于点C,D,且AB=AD,连结BC并延长至E,使∠PEB=∠PAB.分析 (Ⅰ)证连结DC,只要判断△PEC≌△PDC,利用三角形全等的性质即得.
(Ⅱ)判断△ABC∽△APB,利用全等的性质得到AB2=AP•AC=AP(AP-PC),进一步得到$A{P^2}-2A{B^2}=AB•BD=\sqrt{3}$,解得;
解答 (Ⅰ)证明:连结DC,
因为∠PCE=∠ACB=∠ADB,∠PCD=∠ABD,又因为AB=AD,
所以∠ABD=∠ADB,
所以∠PCE=∠PCD…(3分)
由已知∠PEB=∠PAB,∠PDC=∠PAB,
所以∠PEC=∠PDC,且PC=PC,
所以△PEC≌△PDC,所以PE=PD…(5分)
(Ⅱ)因为∠ACB=∠PBA,∠BAC=∠PAB
所以△ABC∽△APB,则AB2=AP•AC=AP(AP-PC),
所以AP2-AB2=AP•PC=PD•PB=PD(PD+BD)
又因为PD=AB,AB=1,所以$A{P^2}-2A{B^2}=AB•BD=\sqrt{3}$,…(8分)
所以$A{P^2}=2+\sqrt{3}$.
所以 $AP=\frac{{\sqrt{2}+\sqrt{6}}}{2}$…(10分)
点评 本题考查了三角形全等和相似的判定定理和性质定理的运用,通过圆的有关性质得到线段之间的关系是关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=-x2 | B. | f(x)=$\frac{1}{{x}^{2}}$ | C. | f(x)=$\frac{1}{{x}^{3}}$ | D. | f(x)=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
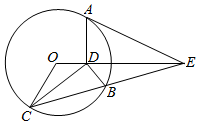 如图,AE是圆O的切线,A是切点,AD与OE垂直,垂足是D,割线EC交圆O于B,C,且∠ODC=α,∠DBC=β,则∠OEC=β-α(用α,β表示).
如图,AE是圆O的切线,A是切点,AD与OE垂直,垂足是D,割线EC交圆O于B,C,且∠ODC=α,∠DBC=β,则∠OEC=β-α(用α,β表示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ($\sqrt{2}$,+∞) | B. | ($\sqrt{3}$,+∞) | C. | ($\sqrt{2}$+1,+∞) | D. | ($\sqrt{3}$+1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com