
(本小题满分12分)根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
社团 | 街舞 | 围棋 | 武术 |
人数 | 320 | 240 | 200 |
社团抽取的同学8人。
(Ⅰ) 求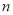 的值和从“围棋”社团抽取的同学的人数;
的值和从“围棋”社团抽取的同学的人数;
(Ⅱ)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知 “围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率。
(Ⅰ)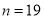 , 从“围棋”社团抽取的同学为6人;(Ⅱ)
, 从“围棋”社团抽取的同学为6人;(Ⅱ)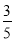 .
.
【解析】
试题分析:(Ⅰ)首先根据“街舞”社团所抽取的人数求出抽样比,从而得出样本容量 和“围棋”社团抽取的同学的人数;
和“围棋”社团抽取的同学的人数;
(Ⅱ) 由(Ⅰ)知,从“围棋”社团抽取的同学为6人,其中2位女生记为A,B,4位男生记为C,D,E,F,从中选出2人担任该社团活动监督的职务有15种不同的结果,由于是任意选取的,每个结果出现的可能性是相等的,所以可利用古典概型号的概率公式求出至少有1名女同学被选为监督职务的概率.
试题解析:(Ⅰ)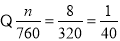
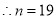 2分
2分
从“围棋”社团抽取的同学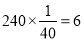 4分
4分
(Ⅱ)由(Ⅰ)知,从“围棋”社团抽取的同学为6人,
其中2位女生记为A,B,4位男生记为C,D,E,F 5分
则从这6位同学中任选2人,不同的结果有
{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},
{C,D},{C,E},{C,F},{D,E},{D,F},{E,F},
共15种. 8分
法1:其中含有1名女生的选法为
{A,C},{A,D},{A,E},{A,F},
{B,C},{B,D},{B,E},{B,F},
共8种;
含有2名女生的选法只有{A,B}1种. 至少有1名女同学共9种 10分
故至少有1名女同学被选中的概率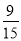 =
=
 . 12分
. 12分
法2:从这6位同学中任选2人,没有女生的有:{C,D},{C,E},{C,F},{D,E},{D,F},
{E,F},共6种
故至少有1名女同学被选中的概率1- =
=
 .
.
考点:1、分层抽样;2、古典概型.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考文科数学试卷(解析版) 题型:选择题
下列算法中,含有条件分支结构的是( )
A.求两个数的积
B.求点到直线的距离
C.解一元二次不等式
D.已知梯形两底和高求面积
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测文科数学试卷(解析版) 题型:选择题
设l为直线,?,?是两个不同的平面,下列命题中正确的是
A.若l//?,l//?,则?//? B.若?//?,l//?,则l//?
C.若l??,l//?,则??? D.若???,l//?,则l??
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测理科数学试卷(解析版) 题型:选择题
设条件p: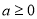 ;条件q:
;条件q: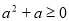 ,那么p是q的
,那么p是q的
A.充分条件 B.必要条件 C.充要条件 D.非充分非必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省四地六校高三上学期第三次月考理科数学试卷(解析版) 题型:填空题
如图,一个几何体的三视图是三个直角三角形,则该几何体的外接球的表面积为 .

查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省绥化市三校高二上学期期中联考数学试卷(解析版) 题型:填空题
过抛物线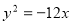 的焦点作直线
的焦点作直线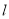 ,直线
,直线 交抛物线于
交抛物线于 两点,若线段AB中点的
两点,若线段AB中点的
横坐标为 ,则
,则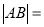 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com