
| A. | 正方形是平行四边形 | B. | 平行四边形的对角线相等 | ||
| C. | 正方形的对角线相等 | D. | 以上均不正确 |
分析 三段论是由两个含有一个共同项的性质判断作前提得出一个新的性质判断为结论的演绎推理.在三段论中,含有大项的前提叫大前提,如本例中的“平行四边形的对角线相等”;含有小项的前提叫小前提,如本例中的“正方形是平行四边形”.另外一个是结论.
解答 解:由演绎推理三段论可得
本例中的“平行四边形的对角线相等”为大前提;
本例中的“正方形是平行四边形”为小前提;
则结论为“正方形的对角线相等”
故选C.
点评 三段论推理是演绎推理中的一种简单判断推理.它包含两个性质判断构成的前提,和一个性质判断构成的结论.一个正确的三段论有仅有三个词项,其中联系大小前提的词项叫中项;出现在大前提中,又在结论中做谓项的词项叫大项;出现在小前提中,又在结论中做主项的词项叫小项.


科目:高中数学 来源: 题型:解答题
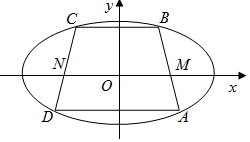 如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$
如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\int_0^1{xdx}$ | B. | ${∫}_{0}^{1}$(x+1)dx | C. | ${∫}_{0}^{1}$1dx | D. | ${∫}_{0}^{1}$$\frac{1}{2}$dx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 开车时使用手机 | 开车时不使用手机 | 合计 | |
| 男性司机人数 | |||
| 女性司机人数 | |||
| 合计 |
| P(Χ2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com