
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
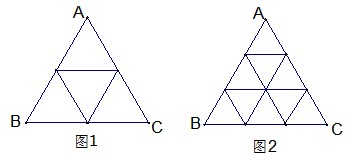
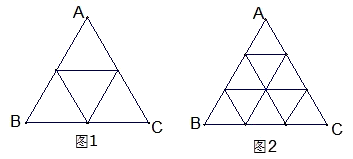
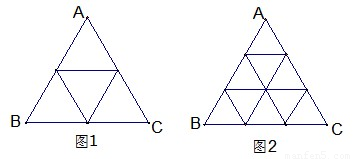
在边长为a的正三角形的三个角处各剪去一个四边形.这个四边形是由两个全等的直角三角形组成的,并且这三个四边形也全等,如图①.若用剩下的部分折成一个无盖的正三棱柱形容器,如图②.则当容器的高为多少时,可使这个容器的容积最大,并求出容积的最大值.
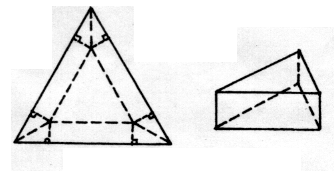
图① 图②
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年上海市浦东新区建平中学高三(上)12月月考数学试卷(文理合卷)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com