
 (
( 且
且 )的图象过点
)的图象过点 ,点
,点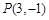 关于直线
关于直线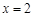 的对称点
的对称点 在
在 的图象上.
的图象上. 的解析式;
的解析式;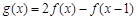 ,求
,求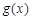 的最小值及取得最小值时x的值.
的最小值及取得最小值时x的值.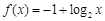 .(Ⅱ)当
.(Ⅱ)当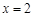 时,函数
时,函数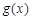 取得最小值1.
取得最小值1. 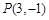 关于直线
关于直线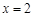 的对称点Q的坐标为
的对称点Q的坐标为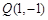 .再由由
.再由由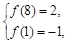 得
得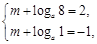 得到参数m,a的值,求得解析式。
得到参数m,a的值,求得解析式。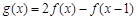
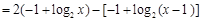
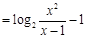 (
(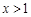 ),然后利用均值不等式得到最值。
),然后利用均值不等式得到最值。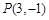 关于直线
关于直线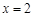 的对称点Q的坐标为
的对称点Q的坐标为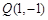 .·········· 2分
.·········· 2分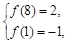 得
得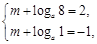 ······················· 4分
······················· 4分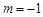 ,
,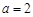 ,故函数解析式为
,故函数解析式为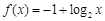 .············ 6分
.············ 6分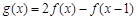
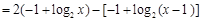
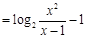 (
(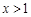 ),
),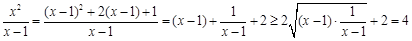 ,
,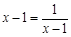 即
即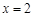 时,“=”成立, ················ 10分
时,“=”成立, ················ 10分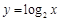 在
在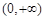 上单调递增,则
上单调递增,则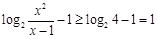 ,
,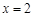 时,函数
时,函数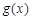 取得最小值1.··················· 12分
取得最小值1.··················· 12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com