练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，圆O与圆O′内切于点T，点P为外圆O上任意一点，PM与内圆O′切于点M.求证：PM∶PT为定值．

     

     

    见解析

    【解析】证明：设外圆半径为R，内圆半径为r，作两圆的公切线TQ.

    设PT交内圆于C，连结OP，O′C，则PM2＝PC·PT，所以.

    由弦切角定理知∠POT＝2∠PTQ，∠CO′T＝2∠PTQ，

    则∠POT＝∠CO′T，所以PO∥CO′，

    所以，即，为定值．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－4第2课时练习卷（解析版） 题型：解答题

    用数学归纳法证明：当n是不小于5的自然数时，总有2n>n2成立．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－2第2课时练习卷（解析版） 题型：解答题

    用解方程组的方法求下列矩阵M的逆矩阵．

    (1)M＝；(2)M＝.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－2第1课时练习卷（解析版） 题型：解答题

    二阶矩阵M对应变换将(1，－1)与(－2，1)分别变换成(5，7)与(－3，6)．

    (1)求矩阵M；

    (2)若直线l在此变换下所变换成的直线的解析式l′：11x－3y－68＝0，求直线l的方程．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－2第1课时练习卷（解析版） 题型：解答题

    点(－1，k)在伸压变换矩阵之下的对应点的坐标为(－2，－4)，求m、k的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－1第2课时练习卷（解析版） 题型：解答题

    如图，PA切圆O于点A，割线PBC交圆O于点B、C，∠APC的角平分线分别与AB、AC相交于点D、E，求证：

    (1)AD＝AE；

    (2)AD2＝DB·EC.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－1第2课时练习卷（解析版） 题型：解答题

    如图，AB是圆O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F.求证：∠DEA＝∠DFA.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－1第1课时练习卷（解析版） 题型：解答题

    已知：如图，在等腰梯形ABCD中，AD∥BC，AB＝DC，过点D作AC的平行线DE，交BA的延长线于点E.求证：

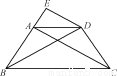
    (1)△ABC≌△DCB；

    (2)DE·DC＝AE·BD.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第十章第5课时练习卷（解析版） 题型：填空题

    设集合A＝{1，2}，B＝{1，2，3}，分别从集合A和B中随机取一个数a和b，确定平面上的一个点P(a，b)，记“点P(a，b)落在直线x＋y＝n上”为事件Cn(2≤n≤5，n∈N)，若事件Cn的概率最大，则n的所有可能值为________．

     

    查看答案和解析>>

    同步练习册答案