
已知动直线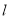 与椭圆
与椭圆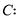
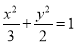 交于
交于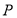
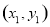 、
、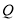
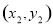 两不同点,且△
两不同点,且△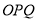 的面积
的面积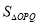 =
=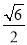 ,其中
,其中 为坐标原点.
为坐标原点.
(1)证明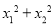 和
和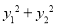 均为定值;
均为定值;
(2)设线段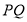 的中点为
的中点为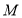 ,求
,求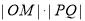 的最大值;
的最大值;
(3)椭圆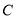 上是否存在点
上是否存在点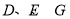 ,使得
,使得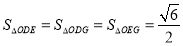 ?若存在,判断△
?若存在,判断△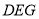 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.
(1)证明详见解析;(2)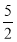 ;(3)不存在点
;(3)不存在点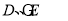 满足要求.
满足要求.
【解析】
试题分析:(1)先检验直线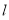 斜率不存在的情况,后假设直线
斜率不存在的情况,后假设直线 的方程,利用弦长公式求出
的方程,利用弦长公式求出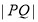 的长,利用点到直线的距离公式求点
的长,利用点到直线的距离公式求点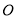 到直线
到直线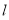 的距离,根据三角形的面积公式,即可求得
的距离,根据三角形的面积公式,即可求得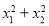 与
与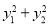 均为定值;(2)由(1)可求线段
均为定值;(2)由(1)可求线段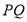 的中点
的中点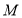 的坐标,代入
的坐标,代入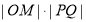 并利用基本不等式求最值;(3)假设存在
并利用基本不等式求最值;(3)假设存在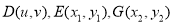 ,使得
,使得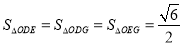 ,由(1)得
,由(1)得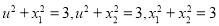 ,
,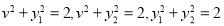 ,从而求得点
,从而求得点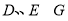 的坐标,可以求出直线
的坐标,可以求出直线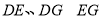 的方程,从而得到结论.
的方程,从而得到结论.
试题解析:(1)当直线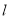 的斜率不存在时,P,Q两点关于
的斜率不存在时,P,Q两点关于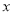 轴对称,所以
轴对称,所以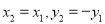
因为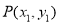 在椭圆上,因此
在椭圆上,因此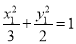 ①
①
又因为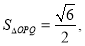 所以
所以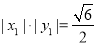 ②
②
由①、②得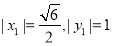 ,此时
,此时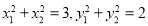 2分
2分
当直线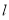 的斜率存在时,设直线
的斜率存在时,设直线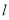 的方程为
的方程为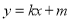
由题意知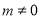 ,将其代入
,将其代入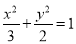 ,得
,得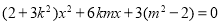
其中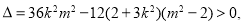 即
即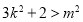 (*)
(*)
又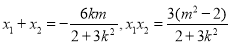
所以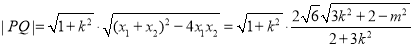
因为点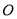 到直线
到直线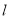 的距离为
的距离为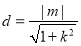
所以
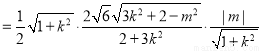
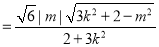
又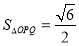 ,整理得
,整理得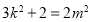 ,且符合(*)式
,且符合(*)式
此时
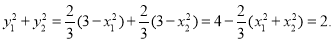
综上所述,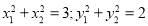 结论成立 5分
结论成立 5分
(2)解法一:
(1)当直线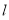 的斜率不存在时,由(I)知
的斜率不存在时,由(I)知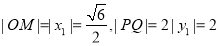
因此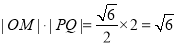 6分
6分
(2)当直线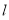 的斜率存在时,由(I)知
的斜率存在时,由(I)知
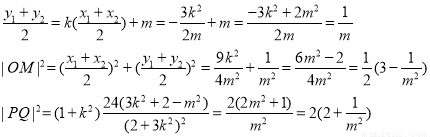
所以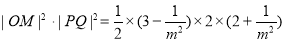
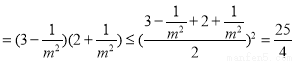
所以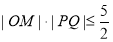 ,当且仅当
,当且仅当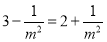 ,即
,即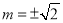 时,等号成立
时,等号成立
综合(1)(2)得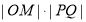 的最大值为
的最大值为 9分
9分
解法二:因为
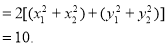
所以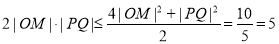
即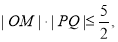 当且仅当
当且仅当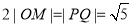 时等号成立
时等号成立
因此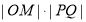 的最大值为
的最大值为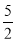 9分
9分
(3)椭圆C上不存在三点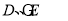 ,使得
,使得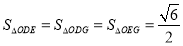 10分
10分
证明:假设存在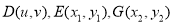 满足
满足
由(I)得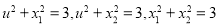
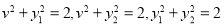
解得
所以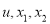 只能从
只能从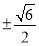 中选取,
中选取, 只能从
只能从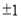 中选取
中选取
因此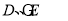 只能在
只能在 这四点中选取三个不同点
这四点中选取三个不同点
而这三点的两两连线中必有一条过原点
与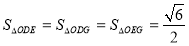 矛盾
矛盾
所以椭圆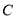 上不存在满足条件的三点
上不存在满足条件的三点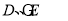 14分.
14分.
考点:1.点到直线的距离公式;2.三角形的面积计算公式;3.直线与椭圆的综合问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末理科数学试卷(解析版) 题型:选择题
已知圆锥的底面半径为 ,高为
,高为 ,在它的所有内接圆柱中,全面积的最大值为( )
,在它的所有内接圆柱中,全面积的最大值为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末文科数学试卷(解析版) 题型:选择题
已知实数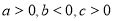 ,则直线
,则直线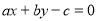 通过( )
通过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
查看答案和解析>>
科目:高中数学 来源:2015届广东惠州高二第一学期期末考试理科数学试卷(解析版) 题型:解答题
某社团组织20名志愿者利用周末和节假日参加社会公益活动,志愿者中,年龄在20至40岁的有12人,年龄大于40岁的有8人.
(1)在志愿者中用分层抽样方法随机抽取5名,年龄大于40岁的应该抽取几名?
(2)上述抽取的5名志愿者中任取2名,求取出的2人中恰有1人年龄大于40岁的概率.
查看答案和解析>>
科目:高中数学 来源:2015届广东惠州高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
已知椭圆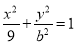
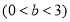 ,左右焦点分别为
,左右焦点分别为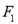 ,
,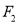 ,过
,过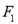 的直线交椭圆于
的直线交椭圆于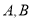 两点,若
两点,若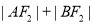 的最大值为8,则
的最大值为8,则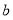 的值是( )
的值是( )
A.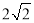 B.
B.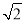 C.
C.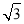 D.
D.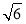
查看答案和解析>>
科目:高中数学 来源:2015届广东台山高二第一学期期末测试文科数学试卷(解析版) 题型:选择题
如图,椭圆
 的左、右顶点分别是
的左、右顶点分别是 ,
, ,左、右焦点分别是
,左、右焦点分别是 ,
, ,若
,若 ,
, ,
, 成等比数列,则此椭圆的离心率为
成等比数列,则此椭圆的离心率为

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com