Question

下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.

x	3	4	5	6
y	2.5	3	4	4.5

(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=;

(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?

(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)

(文)已知某几何体的俯视图是如图8所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.

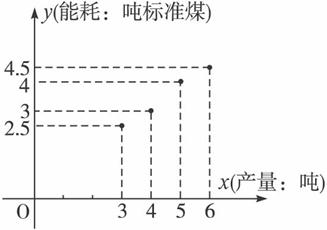
图8

(1)求该几何体的体积V;

(2)求该几何体的侧面积S.

Answer 1

答案：分析:本小题主要考查最小二乘法求线性回归方程、统计量等基础知识,以及数据处理能力、运算求解能力、应用意识.

解：(1)由题设所给数据,可得散点图如上图.

(2)由对照数据,计算得:=86,

=4.5,=3.5,

已知=66.5,所以由最小二乘法确定的回归方程的系数为

=0.7,=3.5-0.7×4.5=0.35.

因此,所求的线性回归方程为y=0.7x+0.35.

(3)由(2)的回归方程及技改前生产100吨甲产品的生产能耗,得降低的生产能耗为90-(0.7×100+0.35)=19.65(吨标准煤).

(文)分析:本小题主要考查三视图、几何体体积、等腰三角形性质、三角形面积等基础知识,以及空间想象能力、运算求解能力.

解：由题设可知几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8、高为h₁的等腰三角形,左、右侧面均为底边长为6、高为h₂的等腰三角形,如上图.

(1)几何体的体积为V=·S_矩形·h=×6×8×4=64.

(2)正侧面及相对侧面底边上的高为h₁==5.

左、右侧面的底边上的高为h₂=.故几何体的侧面面积为

S=2·(×8×5+×6×)=40+2.