
分析 方法一:利用参数分离法转化为求函数的最值问题,利用换元法以判别式法求出即可.
方法二,直接根据基本不等式即可求出.
解答 解:方法一:∵正数x,y满足x+2$\sqrt{2xy}$≤λ(x+y)恒成立,
∴λ≥$\frac{x+2\sqrt{2xy}}{x+y}$=$\frac{1+2\sqrt{2•\frac{y}{x}}}{1+\frac{y}{x}}$恒成立,
设t=$\sqrt{\frac{y}{x}}$,t>0
则函数等价为y=$\frac{1+2\sqrt{2}t}{1+{t}^{2}}$,
∴yt2-2$\sqrt{2}$t+y-1=0,
∴方程有两个正根,
∴$\left\{\begin{array}{l}{△=8-4y(y-1)≥0}\\{\frac{\sqrt{2}}{y}>0}\\{\frac{y-1}{y}>0}\end{array}\right.$,
解得1<y≤2,
∴λ≥2,
故实数λ的最小值为2,
方法二:∵正数x,y满足x+2$\sqrt{2xy}$≤λ(x+y)恒成立,
∴λ≥$\frac{x+2\sqrt{2xy}}{x+y}$.
∵2$\sqrt{2xy}$≤x+2y
∴$\frac{x+2\sqrt{2xy}}{x+y}$≤$\frac{x+x+2y}{x+y}$=2,
∴λ≥2,
故实数λ的最小值为2,
故答案为:2
点评 本题主要考查不等式恒成立问题,利用参数分离法以及换元法,转化为求函数的最值是解决本题的关键.综合性较强,运算量较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
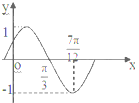 把函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位得到y=f(x)的图象(如图),则2A-ω+φ=( )
把函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{3}$个单位得到y=f(x)的图象(如图),则2A-ω+φ=( )| A. | $-\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | $-\frac{π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{11}$ | C. | -$\frac{1}{13}$ | D. | -$\frac{1}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
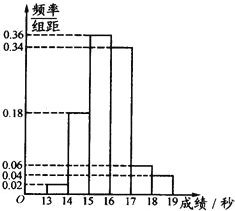 某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,如图是测试成绩频率分布直方图.成绩小于17秒的学生人数为( )
某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,如图是测试成绩频率分布直方图.成绩小于17秒的学生人数为( )| A. | 45 | B. | 35 | C. | 17 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com