
| A. | ?a∈R,函数f(x)是奇函数 | B. | ?a∈R,函数f(x)是偶函数 | ||
| C. | ?a∈R,函数f(x)在(0,+∞)上是增函数 | D. | ?a∈R,函数f(x)在(0,+∞)上是减函数 |
分析 由题意可得当a=0时,f(x)=$\frac{1}{x}$,f(x)是奇函数,且函数f(x)在(0,+∞)上是减函数,排除A,B;再根据当a<0,函数f(x)为减函数,故排除C,从而得出结论.
解答 解:对于函数f(x)=ax2+$\frac{1}{x}$,当a=0时,f(x)=$\frac{1}{x}$,此时,f(x)是奇函数,
且函数f(x)在(0,+∞)上是减函数;
当a≠0时,函数f(x)=ax2+$\frac{1}{x}$为非奇非偶函数,故排除A,B.
当a<0,在(0,+∞)上,f′(x)=2ax-$\frac{1}{{x}^{2}}$<0,函数f(x)为减函数,故排除C,
故选:D.
点评 本题主要考查函数的奇偶性、单调性的判断和证明,利用导数研究函数的单调性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | -1 | C. | 1 | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
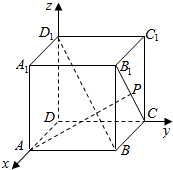 如图所示,正方体ABCD-A1B1C1D1的棱长为1,以D为原点,以正方体的三条棱DA,DC,DD1所在的直线分别为x轴,y轴,z轴建立空间直角坐标系,若点P在正方体的侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则下列点P的坐标①(1,1,1),②(0,1,0),③(1,1,0),④(0,1,1),⑤($\frac{1}{2}$,1,$\frac{1}{2}$)中正确的是①②⑤.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,以D为原点,以正方体的三条棱DA,DC,DD1所在的直线分别为x轴,y轴,z轴建立空间直角坐标系,若点P在正方体的侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则下列点P的坐标①(1,1,1),②(0,1,0),③(1,1,0),④(0,1,1),⑤($\frac{1}{2}$,1,$\frac{1}{2}$)中正确的是①②⑤.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com