
【题目】己知数列![]() :1,
:1,![]() ,
,![]() ,3,3,3,
,3,3,3,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,即当
,即当![]() (
(![]() )时,
)时,![]() ,记
,记![]() (
(![]() ).
).
(1)求![]() 的值;
的值;
(2)求当![]() (
(![]() ),试用n、k的代数式表示
),试用n、k的代数式表示![]() (
(![]() );
);
(3)对于![]() ,定义集合
,定义集合![]() 是
是![]() 的整数倍,
的整数倍,![]() ,且
,且![]() ,求集合
,求集合![]() 中元素的个数.
中元素的个数.
【答案】(1)1888;(2)![]() ,
,![]() (
(![]() );(3)65.
);(3)65.
【解析】
(1)令![]() ,解得
,解得![]() ,分析规律可得,
,分析规律可得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,由此即可求出
,由此即可求出![]() ;
;
(2)当![]() (
(![]() )时,
)时,![]() ,分别求出
,分别求出![]() 为奇数时和
为奇数时和![]() 为偶数时
为偶数时![]() 的表达式,最后用n、k的代数式表示
的表达式,最后用n、k的代数式表示![]() 即可;
即可;
(3)首先![]() 时,
时,![]() ,满足条件,故
,满足条件,故![]() ,此时n取1个整数,由(2)知,当
,此时n取1个整数,由(2)知,当![]() (
(![]() )时,可得
)时,可得![]() ,由
,由![]() 可得,
可得,![]() 必为偶数,令
必为偶数,令![]() ,解得
,解得![]() ,从而依次令
,从而依次令![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,结合
,结合![]() ,分别求出n取整数的个数即可得到最终结果.
,分别求出n取整数的个数即可得到最终结果.
(1)依题意,令![]() (
(![]() ),解得
),解得![]() ,
,
分析规律可得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]()
![]()
![]()
![]() ;
;
(2)当![]() (
(![]() )时,
)时,
![]() ,
,
若![]() 为奇数,
为奇数,
![]()
![]()
![]() ;
;
若![]() 为偶数,
为偶数,
![]()
![]()
![]() .
.
综上所述,![]() ,
,![]() (
(![]() );
);
(3)首先![]() 时,
时,![]() ,满足条件,故
,满足条件,故![]() ,此时n取1个整数;
,此时n取1个整数;
由(2)知,当![]() (
(![]() )时,
)时,
![]() ,又
,又![]() ,
,
则 ,
,
由![]() 可得,
可得,![]() 必为偶数,
必为偶数,
令![]() ,解得
,解得![]() ,所以有:
,所以有:
当![]() 时,因为
时,因为![]() ,故n可取3个整数;
,故n可取3个整数;
当![]() 时,因为
时,因为![]() ,故n可取5个整数;
,故n可取5个整数;
当![]() 时,因为
时,因为![]() ,故n可取7个整数;
,故n可取7个整数;
![]()
当![]() 时,因为
时,因为![]() ,故n可取63个整数;
,故n可取63个整数;
综上,集合![]() 中元素的个数为:
中元素的个数为:![]()


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
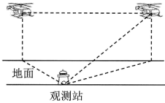
【题目】2019年10月1日,在庆祝新中国成立70周年阅兵中,由我国自主研制的军用飞机和军用无人机等参阅航空装备分秒不差飞越天安门,壮军威,振民心,令世人瞩目.飞行员高超的飞行技术离不开艰苦的训练和科学的数据分析.一次飞行训练中,地面观测站观测到一架参阅直升飞机以![]() 千米/小时的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西
千米/小时的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西![]() 的方向上,1分钟后第二次观测到该飞机在北偏东
的方向上,1分钟后第二次观测到该飞机在北偏东![]() 的方向上,仰角为
的方向上,仰角为![]() ,则直升机飞行的高度为________千米.(结果保留根号)
,则直升机飞行的高度为________千米.(结果保留根号)
查看答案和解析>>
科目:高中数学 来源: 题型:
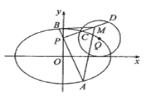
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() 、
、![]() ,
,![]() ,若圆Q方程
,若圆Q方程![]() ,且圆心Q在椭圆上.
,且圆心Q在椭圆上.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 交椭圆
交椭圆![]() 于A、B两点,过直线
于A、B两点,过直线![]() 上一动点P作与
上一动点P作与![]() 垂直的直线
垂直的直线![]() 交圆Q于C、D两点,M为弦CD中点,
交圆Q于C、D两点,M为弦CD中点,![]() 的面积是否为定值?若为定值,求出此定值;若不为定值,说明你的理由.
的面积是否为定值?若为定值,求出此定值;若不为定值,说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若关于![]() 的方程f(x)=kex(其中e为自然对数的底数)恰有两个不同的实根,求实数
的方程f(x)=kex(其中e为自然对数的底数)恰有两个不同的实根,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
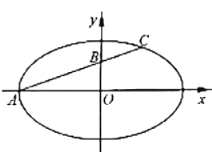
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,过
,过![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若椭圆![]() 的焦距为
的焦距为![]() ,
,![]() 为椭圆
为椭圆![]() 上一点,线段
上一点,线段![]() 的垂直平分线
的垂直平分线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() (
(![]() 不与
不与![]() 轴重合),求直线
轴重合),求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com