
分析 (1)设M(x,y),利用直线AM的斜率与直线BM的斜率的差为-2,建立方程,即可求得点M的轨迹C的方程;
(2)设点$P(x,1-{x^2}),Q({x_0},1-{x_0}^2)$,由题意AP⊥PQ,通过向量的数量积为0,列出方程,然后求解点Q的横坐标的取值范围.
解答 解:(1)设M(x,y),则kAM=$\frac{y}{x+1}$,kBM=$\frac{y}{x-1}$
∵直线AM的斜率与直线BM的斜率的差为-2,$\frac{y}{x+1}$-$\frac{y}{x-1}$=-2
∴y=1-x2(y≠0)(或x≠±1).
(2)设点$P(x,1-{x^2}),Q({x_0},1-{x_0}^2)$,知$\overrightarrow{AP}=(x+1,1-{x^2}),\overrightarrow{PQ}=({x_0}-x,{x^2}-{x_0}^2)$,
由题意可知1+(x-1)(x+x0)=0从而${x_0}=-\frac{1}{x-1}-x$,
当x>1时,${x_0}=-(\frac{1}{x-1}+x-1)-1≤-3$当x<1时,${x_0}=-(\frac{1}{x-1}+x-1)-1≥1$,
由于x≠±1,且x0≠±1,故x≠-1有${x_0}≠\frac{3}{2}$.
所以点Q的横坐标的取值范围是:$(-∞,-3]∪(1,\frac{3}{2})∪(\frac{3}{2},+∞)$.
点评 本题考查轨迹方程的求法,考查抛物线的定义,考查直线与圆的位置关系,正确运用抛物线的定义是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -2 | C. | -$\frac{11}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
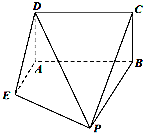 如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-4,-\frac{3}{2})$ | B. | $(-4,-\frac{7}{2})$ | C. | $(-\frac{7}{2},-\frac{3}{2})$ | D. | $(-4,-\frac{7}{2})∪(-\frac{7}{2},-\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,-1) | C. | (-∞,e-3) | D. | (e-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
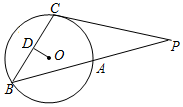 如图,从圆O外一点P引圆的切线PC及割线PAB,C为切点,OD⊥BC,垂足为D.
如图,从圆O外一点P引圆的切线PC及割线PAB,C为切点,OD⊥BC,垂足为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com