
| A. | $(-4,-\frac{3}{2})$ | B. | $(-4,-\frac{7}{2})$ | C. | $(-\frac{7}{2},-\frac{3}{2})$ | D. | $(-4,-\frac{7}{2})∪(-\frac{7}{2},-\frac{3}{2})$ |
分析 作出f(x)的图象,结合图象,得(-∞,-1),(0,1)是增区间,(-1,0),(1,+∞)是减区间,当x=±1时,f(x)取最大值是2,;当x=0时,f(x)取最小值是0,y=$\frac{3}{2}$是部分图象的渐近线.设t=f(x),由此能求出实数a的取值范围.
解答 解:∵定义在R上的函数y=f(x)是偶函数,当x≥0时,$f(x)=\left\{{\begin{array}{l}{2sin\frac{π}{2}x,0≤x≤1}\\{{{(\frac{1}{2})}^x}+\frac{3}{2},x>1}\end{array}}\right.$
∴f(x)的图象如图所示,
结合图象,得(-∞,-1),(0,1)是增区间,(-1,0),(1,+∞)是减区间,
当x=±1时,f(x)取最大值是2,;
当x=0时,f(x)取最小值是0,
$y=\frac{3}{2}$是部分图象的渐近线.
设t=f(x),依题意,符合题意有两种情况:
①t1=2,${t_2}∈(\frac{3}{2},2)$,此时$-a={t_1}+{t_2}∈(\frac{7}{2},4)$,则$a∈(-4,-\frac{7}{2})$;
②${t_1}∈(0,\frac{3}{2}]$,${t_2}∈(\frac{3}{2},2)$,此时$-a={t_1}+{t_2}∈(\frac{3}{2},\frac{7}{2})$,则$a∈(-\frac{7}{2},-\frac{3}{2})$;
综上,实数a的取值范围是$a∈(-4,-\frac{7}{2})∪(-\frac{7}{2},-\frac{3}{2})$.
故选:D.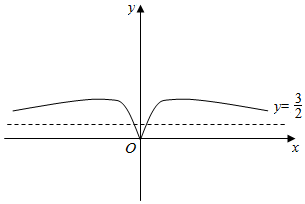
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意函数的图象、性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 2R | B. | R | ||
| C. | 4R | D. | $\frac{1}{2}$R(R为△ABC外接圆半径) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
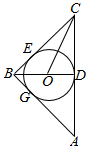 已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=2$\sqrt{2}$,AC-4
已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=2$\sqrt{2}$,AC-4查看答案和解析>>
科目:高中数学 来源: 题型:解答题
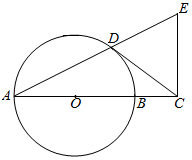 如图,已知AB是⊙O的直径,点D是⊙O上一点,过点D作⊙O的切线,交AB的延长线于点C,过点C作AC的垂线,交AD的延长线于点E.
如图,已知AB是⊙O的直径,点D是⊙O上一点,过点D作⊙O的切线,交AB的延长线于点C,过点C作AC的垂线,交AD的延长线于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com