
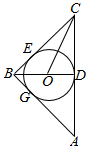 已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=2$\sqrt{2}$,AC-4
已知圆O是△ABC的内切圆,与AC,BC分别切于D,E两点,如图所示,连接BD交圆O于点G,BC=BA=2$\sqrt{2}$,AC-4分析 (Ⅰ)连结DE,∠CBA的平分线与AC边上的中线重合,圆心O在直线BD上,CO是∠ECD的角平分线,由此能证明EG∥CO.
(Ⅱ)AD=DC=2,且∠BDC=90°,由勾股定理得BD=2,由圆的切线长定理,得BE=2$\sqrt{2}-2$,再由切割线定理能求出BG.
解答 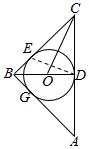 证明:(Ⅰ)连结DE,∵BC=BA,∴∠CBA的平分线与AC边上的中线重合,
证明:(Ⅰ)连结DE,∵BC=BA,∴∠CBA的平分线与AC边上的中线重合,
三角形的内切圆的圆心是三条角平分线的交点,
∴圆心O在直线BD上,
∴GD为圆O的直径,∴EG⊥ED,∴CO是∠ECD的角平分线,
又⊙O与AC、BC分别相切于D、E两点,
∴CE=CD,∴ED⊥CO,
∴EG∥CO.
解:(Ⅱ)由(Ⅰ)知:AD=DC=$\frac{1}{2}$AC=2,且∠BDC=90°,
在Rt△BDC中,由勾股定理得:BD2=BC2-CD2=(2$\sqrt{2}$)2-22=4,
∴BD=2,
由圆的切线长定理,得CE=CD=2,
∴BE=2$\sqrt{2}-2$,
由切割线定理得BE2=BG•BD,即(2$\sqrt{2}-2$)2=BG•2,
解得BG=6-4$\sqrt{2}$.
点评 本题考查两直线平行的证明,考查线段长的求法,是中档题,解题时要认真审题,注意勾股定理、切线长定理、切割线定理的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-4,-\frac{3}{2})$ | B. | $(-4,-\frac{7}{2})$ | C. | $(-\frac{7}{2},-\frac{3}{2})$ | D. | $(-4,-\frac{7}{2})∪(-\frac{7}{2},-\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,-1) | C. | (-∞,e-3) | D. | (e-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
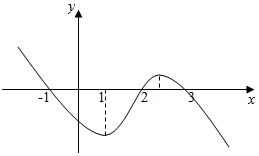 已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( )
已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( )| A. | (1,2)∪($\frac{5}{2}$,3)∪(-∞,-1) | B. | (-∞,-1)∪($\frac{5}{2}$,3) | C. | (-∞,-1)∪(3,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$π | B. | $\frac{8\sqrt{6}}{27}$π | C. | $\frac{16}{3}$π | D. | $\frac{32\sqrt{6}}{27}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
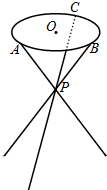 如图,小凳的凳面为圆形,凳脚为三根细钢管,考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点P与凳面圆心O的连线垂直于凳面和地面,且P分细钢管上下两端的比值为0.618,三只凳脚与地面所成的角均为60°,若A、B、C是凳面圆角的三等分点,AB=18厘米,求凳面的高度h及三根细钢管的总长度(精确到0.01)
如图,小凳的凳面为圆形,凳脚为三根细钢管,考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点P与凳面圆心O的连线垂直于凳面和地面,且P分细钢管上下两端的比值为0.618,三只凳脚与地面所成的角均为60°,若A、B、C是凳面圆角的三等分点,AB=18厘米,求凳面的高度h及三根细钢管的总长度(精确到0.01)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com