
分析 (1)直接利用向量共线列出方程,利用正弦定理以及余弦定理直接求解即可.
(2)利用两角和与差的三角函数以及二倍角公式直接求解即可.
解答 解:(1)△ABC的内角A,B,C对边分别为a,b,c,已知向量$\overrightarrow{m}$=(b,2c),$\overrightarrow{n}$=(sinB,sinA),且$\overrightarrow{m}$∥$\overrightarrow{n}$,可得:2csinB=bsinA,由正弦定理可得:2bc=ba,c=3可得a=2c=6,cosB=$\frac{1}{3}$.
由余弦定理可得:b2=a2+c2-2accosB=36+9-2×$3×6×\frac{1}{3}$=33,
b=$\sqrt{33}$.
(2)$cos(2B-\frac{π}{6})$=cos2Bcos$\frac{π}{6}$+sin2Bsin$\frac{π}{6}$=(2cos2B-1)×$\frac{\sqrt{3}}{2}$+2sinBcosB×$\frac{1}{2}$
=($2×\frac{1}{9}-1$)×$\frac{\sqrt{3}}{2}$+$\frac{2\sqrt{2}}{3}×\frac{1}{3}$
=$\frac{4\sqrt{2}-7\sqrt{3}}{18}$.
点评 本题考查正弦定理的应用,两角和与差的三角函数,以及同角三角函数的基本关系式的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
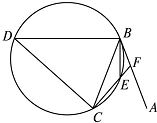 直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-4,-\frac{3}{2})$ | B. | $(-4,-\frac{7}{2})$ | C. | $(-\frac{7}{2},-\frac{3}{2})$ | D. | $(-4,-\frac{7}{2})∪(-\frac{7}{2},-\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
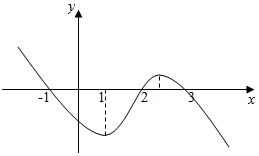 已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( )
已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( )| A. | (1,2)∪($\frac{5}{2}$,3)∪(-∞,-1) | B. | (-∞,-1)∪($\frac{5}{2}$,3) | C. | (-∞,-1)∪(3,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知球O与正四棱柱ABCD-A1B1C1D1的底面ABCD及四个侧面都相切,对角线BD1与球面的两个交点分别为M,N,M为线段BD的中点,MN=$\sqrt{6}$.则球O的体积为$\frac{9}{2}$π.
已知球O与正四棱柱ABCD-A1B1C1D1的底面ABCD及四个侧面都相切,对角线BD1与球面的两个交点分别为M,N,M为线段BD的中点,MN=$\sqrt{6}$.则球O的体积为$\frac{9}{2}$π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com