
 已知球O与正四棱柱ABCD-A1B1C1D1的底面ABCD及四个侧面都相切,对角线BD1与球面的两个交点分别为M,N,M为线段BD的中点,MN=$\sqrt{6}$.则球O的体积为$\frac{9}{2}$π.
已知球O与正四棱柱ABCD-A1B1C1D1的底面ABCD及四个侧面都相切,对角线BD1与球面的两个交点分别为M,N,M为线段BD的中点,MN=$\sqrt{6}$.则球O的体积为$\frac{9}{2}$π. 分析 求出cos∠BD1D=$\frac{4R}{2\sqrt{6}R}$=$\frac{\sqrt{6}}{3}$,取MN的中点E,则ME=$\frac{\sqrt{6}}{2}$,利用cos∠OME=cos∠BD1D=$\frac{\sqrt{6}}{3}$=$\frac{\frac{\sqrt{6}}{2}}{R}$,求出R,即可求出球O的体积.
解答 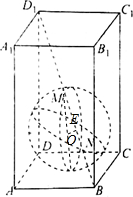 解:由题意,M为线段BD的中点,∴DD1=4R,
解:由题意,M为线段BD的中点,∴DD1=4R,
∵BD=2$\sqrt{2}$R,∴BD1=$\sqrt{16{R}^{2}+8{R}^{2}}$=2$\sqrt{6}$R,
∴cos∠BD1D=$\frac{4R}{2\sqrt{6}R}$=$\frac{\sqrt{6}}{3}$,
取MN的中点E,则ME=$\frac{\sqrt{6}}{2}$,
∴cos∠OME=cos∠BD1D=$\frac{\sqrt{6}}{3}$=$\frac{\frac{\sqrt{6}}{2}}{R}$,
∴R=$\frac{3}{2}$,
∴球O的体积为$\frac{4}{3}π{R}^{3}$=$\frac{4}{3}π•(\frac{3}{2})^{3}$=$\frac{9}{2}$π.
故答案为:$\frac{9}{2}$π.
点评 本题考查球O的体积,考查学生的计算能力,正确求出球O的半径是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2 | C. | $\frac{{\sqrt{11}}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
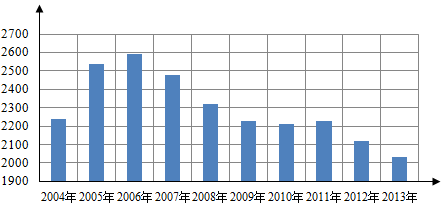
| A. | 2007年我国治理二氧化硫排放显现 | |
| B. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| C. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,一个直角走廊的宽分别为a米、b米,一铁棒欲通过该直角走廊,设铁棒与廊壁成θ角.求:
如图,一个直角走廊的宽分别为a米、b米,一铁棒欲通过该直角走廊,设铁棒与廊壁成θ角.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com