
分析 (1)由题意可得△≥0,x1+x2>0,x1x2>0,解不等式组即可得答案;
(2)设f(x)=x2+2(m-1)x+2m+6,则由题意可得f(2)<0,求解即可得答案.
解答 解:(1)由题意可得$\left\{\begin{array}{l}{△=4(m-1)^{2}-4(2m+6)≥0}\\{{x}_{1}+{x}_{2}=-2(m-1)>0}\\{{x}_{1}{x}_{2}=2m+6>0}\end{array}\right.$,
解得:-3<m<-1;
(2)设f(x)=x2+2(m-1)x+2m+6,则由题意可得f(2)=6m+6<0,
解得:m<-1.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-4,-\frac{3}{2})$ | B. | $(-4,-\frac{7}{2})$ | C. | $(-\frac{7}{2},-\frac{3}{2})$ | D. | $(-4,-\frac{7}{2})∪(-\frac{7}{2},-\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$π | B. | $\frac{8\sqrt{6}}{27}$π | C. | $\frac{16}{3}$π | D. | $\frac{32\sqrt{6}}{27}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
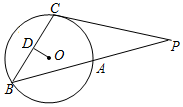 如图,从圆O外一点P引圆的切线PC及割线PAB,C为切点,OD⊥BC,垂足为D.
如图,从圆O外一点P引圆的切线PC及割线PAB,C为切点,OD⊥BC,垂足为D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知球O与正四棱柱ABCD-A1B1C1D1的底面ABCD及四个侧面都相切,对角线BD1与球面的两个交点分别为M,N,M为线段BD的中点,MN=$\sqrt{6}$.则球O的体积为$\frac{9}{2}$π.
已知球O与正四棱柱ABCD-A1B1C1D1的底面ABCD及四个侧面都相切,对角线BD1与球面的两个交点分别为M,N,M为线段BD的中点,MN=$\sqrt{6}$.则球O的体积为$\frac{9}{2}$π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
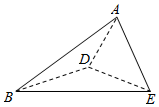 已知三棱锥A-BCD中,△ACD为等边三角形,且平面ACD⊥平面BCD,BD⊥CD,BD=CD=2,则三棱锥A-BCD外接球的表面积为( )
已知三棱锥A-BCD中,△ACD为等边三角形,且平面ACD⊥平面BCD,BD⊥CD,BD=CD=2,则三棱锥A-BCD外接球的表面积为( )| A. | 5π | B. | $\frac{20}{3}$π | C. | 8π | D. | $\frac{28}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
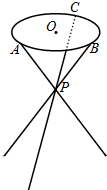 如图,小凳的凳面为圆形,凳脚为三根细钢管,考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点P与凳面圆心O的连线垂直于凳面和地面,且P分细钢管上下两端的比值为0.618,三只凳脚与地面所成的角均为60°,若A、B、C是凳面圆角的三等分点,AB=18厘米,求凳面的高度h及三根细钢管的总长度(精确到0.01)
如图,小凳的凳面为圆形,凳脚为三根细钢管,考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点P与凳面圆心O的连线垂直于凳面和地面,且P分细钢管上下两端的比值为0.618,三只凳脚与地面所成的角均为60°,若A、B、C是凳面圆角的三等分点,AB=18厘米,求凳面的高度h及三根细钢管的总长度(精确到0.01)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 雨 | 雨 | 雨 | 雨 | 雨 | 雨 | |||||||||
| 温度等级 | C | D | C | A | B | C | C | A | D | B | B | C | A | C | A |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 雨 | 雨 | 雨 | 雨 | 雨 | ||||||||||
| 温度等级 | D | C | A | A | D | D | D | B | B | C | D | C | D | D | B |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com