
分析 (Ⅰ)把把C1的参数方程先消去参数化为直角坐标方程,再化为极坐标方程.
(Ⅱ)把曲线C2的极坐标方程化为直角坐标方程,先求出它们的交点的直角坐标,再把它化为极坐标.
解答 解:(Ⅰ)把C1的参数方程$\left\{\begin{array}{l}x={t^2}\\ y=t\end{array}\right.$(t为参数),先消去参数化为直角坐标方程为x=y2,化为极坐标方程为ρcosθ=(ρsinθ)2.
(Ⅱ)曲线C2的极坐标方程为ρ2+2ρcosθ-4=0化为直角坐标方程为x2+y2+2x-4=0,即 (x+1)2+y2=5,
由$\left\{\begin{array}{l}{{y}^{2}=x}\\{{(x+1)}^{2}{+y}^{2}=5}\end{array}\right.$,求得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ 或 $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$,C1与C2交点的直角坐标为(1,1)或(1,-1),
再把它们化为极坐标为($\sqrt{2}$,$\frac{π}{4}$)或($\sqrt{2}$,$\frac{7π}{4}$).
点评 本题主要考查把参数方程、极坐标方程与直角坐标方程的互化,求两条曲线的交点,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
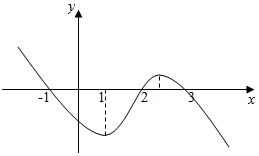 已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( )
已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( )| A. | (1,2)∪($\frac{5}{2}$,3)∪(-∞,-1) | B. | (-∞,-1)∪($\frac{5}{2}$,3) | C. | (-∞,-1)∪(3,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知球O与正四棱柱ABCD-A1B1C1D1的底面ABCD及四个侧面都相切,对角线BD1与球面的两个交点分别为M,N,M为线段BD的中点,MN=$\sqrt{6}$.则球O的体积为$\frac{9}{2}$π.
已知球O与正四棱柱ABCD-A1B1C1D1的底面ABCD及四个侧面都相切,对角线BD1与球面的两个交点分别为M,N,M为线段BD的中点,MN=$\sqrt{6}$.则球O的体积为$\frac{9}{2}$π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
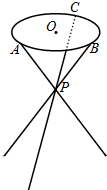 如图,小凳的凳面为圆形,凳脚为三根细钢管,考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点P与凳面圆心O的连线垂直于凳面和地面,且P分细钢管上下两端的比值为0.618,三只凳脚与地面所成的角均为60°,若A、B、C是凳面圆角的三等分点,AB=18厘米,求凳面的高度h及三根细钢管的总长度(精确到0.01)
如图,小凳的凳面为圆形,凳脚为三根细钢管,考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点P与凳面圆心O的连线垂直于凳面和地面,且P分细钢管上下两端的比值为0.618,三只凳脚与地面所成的角均为60°,若A、B、C是凳面圆角的三等分点,AB=18厘米,求凳面的高度h及三根细钢管的总长度(精确到0.01)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 雨 | 雨 | 雨 | 雨 | 雨 | 雨 | |||||||||
| 温度等级 | C | D | C | A | B | C | C | A | D | B | B | C | A | C | A |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 雨 | 雨 | 雨 | 雨 | 雨 | ||||||||||
| 温度等级 | D | C | A | A | D | D | D | B | B | C | D | C | D | D | B |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10π | B. | $\frac{29π}{3}$ | C. | $\frac{28π}{3}$ | D. | $\frac{55π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com