
分析 (Ⅰ)根据${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$化简6Sn=9an-1,得到数列的递推公式后,由等比数列的定义判断出数列{an}是等比数列,由等比数列的通项公式求出an;
(Ⅱ)由周期公式求出ω,由(1)求出最大值即可求出A,由正弦函数的最大值列出方程,由特殊角的三角函数值和φ的范围求出φ,可得f(x)的解析式.
解答 解:(I)由题意得6Sn=9an-1,
当n=1时,6S1=9a1-1,解得a1=$\frac{1}{3}$,
当n≥2时,由6Sn=9an-1 得,6Sn-1=9an-1-1,
两式相减得,6an=9an-9an-1,即an=3an-1,
∴数列{an}是以3为公比,$\frac{1}{3}$为首项的等比数列,
所以${a}_{n}=\frac{1}{3}×{3}^{n-1}={3}^{n-2}$;…(6分)
(II)∵f(x) 的周期为$\pi$,∴ω=2,
由(I)知a3=3,即最大值为3,所以 A=3,
∵f(x) 在$x=\frac{π}{6}$ 处取得最大值,∴$sin({2×\frac{π}{6}+φ})=1$,
则φ+$\frac{π}{3}=\frac{π}{2}+2kπ(k∈Z)$,得φ=$\frac{π}{6}+2kπ(k∈Z)$,
∵$0<φ<\pi$,∴$φ=\frac{π}{6}$,
∴函数f(x) 的解析式为$f(x)=3sin({2x+\frac{π}{6}})$.…(12分)
点评 本题考查了数列前n项和与通项之间的关系式:${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,等比数列的定义、前n项和公式,以及正弦函数的解析式与性质,考查化简、变形能力,属于中档题.


科目:高中数学 来源: 题型:选择题
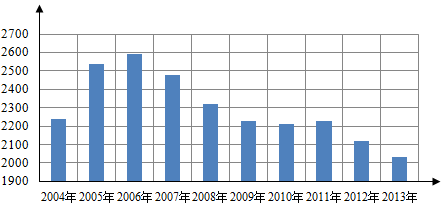
| A. | 2007年我国治理二氧化硫排放显现 | |
| B. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| C. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,一个直角走廊的宽分别为a米、b米,一铁棒欲通过该直角走廊,设铁棒与廊壁成θ角.求:
如图,一个直角走廊的宽分别为a米、b米,一铁棒欲通过该直角走廊,设铁棒与廊壁成θ角.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com