
分析 (1)求得h(x)及h′(x),由题意可知k≥$\frac{5}{2}$,及k=m+$\frac{1}{m}$求得m的取值范围;
(2)求得M(x)及M′(x),采用反证法,假设,函数M(x)在(x0,M(x0))处的切线平行于直线y=1,根据题意列出方程,求得k的解析式,构造辅助函数,利用导数求得函数的单调性及最值,判断与已知是否相符,即可验证是否存在函数M(x)在(x0,M(x0))处的切线平行于直线y=1,
解答 解:因为h(x)=lnx+$\frac{1}{2}$x2-kx;
h′(x)=$\frac{1}{x}$+x-k,
由题意可得:k≥$\frac{5}{2}$,
m+$\frac{1}{m}$=k≥$\frac{5}{2}$,
可得0<m≤$\frac{1}{2}$或m≥2,
综上,m的取值范围为{m丨0<m≤$\frac{1}{2}$或m≥2},
假设,函数M(x)在(x0,M(x0))处的切线平行于直线y=1,
M(x)=f(x)-g(x)=lnx-$\frac{1}{2}$x2+kx,M′(x)=f(x)-g(x)=$\frac{1}{x}$-x+k,
$\left\{\begin{array}{l}{ln{x}_{1}+\frac{1}{2}{x}_{1}^{2}-k{x}_{1}=0}\\{ln{x}_{2}+\frac{1}{2}{x}_{2}^{2}-k{x}_{2}=1}\\{{x}_{1}+{x}_{2}=2{x}_{0}}\\{\frac{1}{{x}_{0}}-{x}_{0}+k=0}\end{array}\right.$,
由ln$\frac{{x}_{1}}{{x}_{2}}$-$\frac{1}{2}$(x1+x2)(x1-x2)=-k(x1-x2),
∴-k=$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$-x0,结合$\frac{1}{{x}_{0}}-{x}_{0}+k=0$,
可得:ln$\frac{{x}_{1}}{{x}_{2}}$=$\frac{2({x}_{1}-{x}_{2})}{{x}_{1}+{x}_{2}}$=$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$,
令u=$\frac{{x}_{1}}{{x}_{2}}$∈(0,1),
∴lnu-$\frac{2(u-1)}{u+1}$=0,u∈(0,1),
设y=lnu-$\frac{2(u-1)}{u+1}$,u∈(0,1),
y′=$\frac{1}{u}$+$\frac{2(u+1)-2(u-1)}{(u+1)^{2}}$=$\frac{(u+1)^{2}-4u}{u(u+1)^{2}}$=$\frac{(u-1)^{2}}{u(u+1)^{2}}$>0,
所以函数y=lnu-$\frac{2(u-1)}{u+1}$,在(0,1)上单调递增,
因此,y<0,即lnu-$\frac{2(u-1)}{u+1}$<0,也就是ln$\frac{{x}_{1}}{{x}_{2}}$<$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$,此时与ln$\frac{{x}_{1}}{{x}_{2}}$=$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$矛盾,
所以
数M(x)在(x0,M(x0))处的切线不能平行于直线y=1,
点评 本题考查函数的导数的综合运用,反正法,根据已知函数关系式,构造辅助函数并根据导数求求单调区间及最值,考查分析问题及解决问题得能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
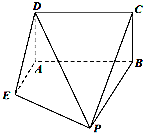 如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-4,-\frac{3}{2})$ | B. | $(-4,-\frac{7}{2})$ | C. | $(-\frac{7}{2},-\frac{3}{2})$ | D. | $(-4,-\frac{7}{2})∪(-\frac{7}{2},-\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
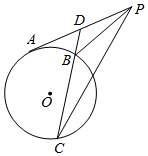 如图,已知PA切⊙O于点A,D为PA的中点,过点D引割线交⊙O于B、C两点.PD=2,PB=3,$DB=\frac{3}{2}$,则PC=4.
如图,已知PA切⊙O于点A,D为PA的中点,过点D引割线交⊙O于B、C两点.PD=2,PB=3,$DB=\frac{3}{2}$,则PC=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,-1) | C. | (-∞,e-3) | D. | (e-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
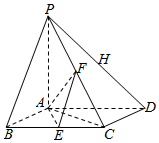 如图,四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,AC=BC,E,F分别是BC,PC的中点.
如图,四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,AC=BC,E,F分别是BC,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
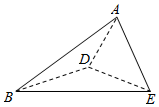 已知三棱锥A-BCD中,△ACD为等边三角形,且平面ACD⊥平面BCD,BD⊥CD,BD=CD=2,则三棱锥A-BCD外接球的表面积为( )
已知三棱锥A-BCD中,△ACD为等边三角形,且平面ACD⊥平面BCD,BD⊥CD,BD=CD=2,则三棱锥A-BCD外接球的表面积为( )| A. | 5π | B. | $\frac{20}{3}$π | C. | 8π | D. | $\frac{28}{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com