
| x2 |
| m |
| x2 |
| n |
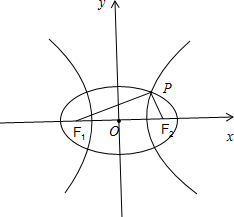 不妨设两曲线的交点P位于双曲线的右支上,设|PF1|=s,|PF2|=t.
不妨设两曲线的交点P位于双曲线的右支上,设|PF1|=s,|PF2|=t.
|
|
| s2+t2-4c2 |
| 2st |
| 2m+2n-4(m-1) |
| 2m-2n |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
| x2 |
| 5 |
| x2 |
| 3 |
| A、锐角三角形 |
| B、B直角三角形 |
| C、钝有三角形 |
| D、等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| m |
| x2 |
| n |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年吉林省高三上学期期末质量检测数学 题型:选择题
(理)已知有相同两焦点F1、F2的椭圆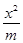 + y2=1(m>1)和双曲线
+ y2=1(m>1)和双曲线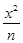 - y2=1(n>0),P是它们的一个交点,则ΔF1PF2的形状是( )
- y2=1(n>0),P是它们的一个交点,则ΔF1PF2的形状是( )
A.锐角三角形 B.直角三角形 C.钝有三角形 D.随m、n变化而变化
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com