
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记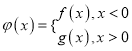 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(i)当![]() 时,若
时,若![]() 在
在![]() ,
, ![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ii)若在点![]() ,
, ![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先求函数导数,转化为研究导函数零点,即方程![]() =0的根的情况,当
=0的根的情况,当![]() ,导函数不变号,在
,导函数不变号,在![]() 上单调递减,当
上单调递减,当![]() 时,有两个不等根,列表分析导函数符号变化规律,确定对应单调区间,(2)(i)利用导数几何意义化简条件:
时,有两个不等根,列表分析导函数符号变化规律,确定对应单调区间,(2)(i)利用导数几何意义化简条件: ![]() 在
在![]() ,
, ![]() 处的切线相互垂直,得
处的切线相互垂直,得![]() ,利用基本不等式证明不等式,(ii)先分别求出切线方程,再根据切线重合得
,利用基本不等式证明不等式,(ii)先分别求出切线方程,再根据切线重合得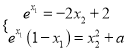 ,消元
,消元![]() 得
得![]() ,利用导数研究函数
,利用导数研究函数![]() ,
, ![]() 单调性,确定函数
单调性,确定函数![]() 值域,进而确定
值域,进而确定![]() 的取值范围.
的取值范围.
试题解析:解:(1)![]() ,则
,则![]() ,
,
当![]() 即
即![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时即
时即![]() 时,
时, ![]() ,
,
此时![]() 在
在![]() 和
和![]() 上都是单调递减的,在
上都是单调递减的,在![]() 上是单调递增的;
上是单调递增的;
(2)(i)![]() ,据题意有
,据题意有![]() ,又
,又![]() ,
,
则![]() 且
且![]() ,
, ![]() ,
,
法1: ![]() ,
,
当且仅当![]() 即
即![]() ,
, ![]() 时取等号.
时取等号.
法2: ![]() ,
, 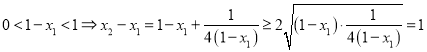 ,
,
当且仅当![]() 时取等号.
时取等号.
(ii)要在点![]() 处的切线重合,首先需要在点
处的切线重合,首先需要在点![]() 处的切线的斜率相等,
处的切线的斜率相等,
而![]() 时,
时, ![]() ,则必有
,则必有![]() ,即
,即![]() ,
, ![]() ,
,
![]() 处的切线方程是:
处的切线方程是: ![]()
![]() 处的切线方程是:
处的切线方程是: ![]() ,
,
即![]() ,
,
据题意则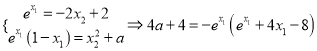 ,
, ![]() ,
,
设![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,
, ![]() 在
在![]() 上恒成立,
上恒成立,
则![]() 在
在![]() 上单调递增
上单调递增![]() ,
,
则![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
则![]() ,再设
,再设![]() ,
, ![]() ,
,
![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
,
则![]() 在
在![]() 恒成立,
恒成立,
即当![]() 时,
时, ![]() 的值域是
的值域是![]() ,
,
故![]() ,即为所求.
,即为所求.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别是a、b、c满足:cosAcosC+sinAsinC+cosB= ![]() ,且a,b,c成等比数列,
,且a,b,c成等比数列,
(1)求角B的大小;
(2)若 ![]() +
+ ![]() =
= ![]() ,a=2,求三角形ABC的面积.
,a=2,求三角形ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.a=9,b=10,A=60°,无解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() ,an=
,an= ![]() (n≥2,n∈N).
(n≥2,n∈N).
(1)试判断数列 ![]() 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(2)设bn= ![]() ,求数列{bn}的前n项和Sn;
,求数列{bn}的前n项和Sn;
(3)设cn=ansin ![]() ,数列{cn}的前n项和为Tn . 求证:对任意的n∈N* , Tn<
,数列{cn}的前n项和为Tn . 求证:对任意的n∈N* , Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,![]() 为前
为前![]() 天两只老鼠打洞之和,则
天两只老鼠打洞之和,则![]() _________________尺.
_________________尺.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com