
【题目】已知数列{an}满足a1= ![]() ,an=
,an= ![]() (n≥2,n∈N).
(n≥2,n∈N).
(1)试判断数列 ![]() 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(2)设bn= ![]() ,求数列{bn}的前n项和Sn;
,求数列{bn}的前n项和Sn;
(3)设cn=ansin ![]() ,数列{cn}的前n项和为Tn . 求证:对任意的n∈N* , Tn<
,数列{cn}的前n项和为Tn . 求证:对任意的n∈N* , Tn< ![]() .
.
【答案】
(1)解:∵ ![]() ,
,
∴ ![]() ,
,
又∵ ![]() ,
,
∴数列 ![]() 是首项为3,公比为﹣2的等比数列.
是首项为3,公比为﹣2的等比数列.
(2)解:依(1)的结论有 ![]() ,
,
即 ![]() .
.
bn=(32n﹣1+1)2=94n﹣1+62n﹣1+1.
![]() .
.
(3)解:∵ ![]() ,
,
∴ ![]() .
.
当n≥3时,
则 ![]() <
< 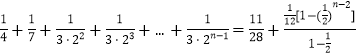
= ![]() .
.
∵T1<T2<T3,
∴对任意的n∈N*, ![]() .
.
【解析】(1)根据题意,对 ![]() 进行变形可得
进行变形可得 ![]() ,从而证得结论;(2)根据(1)求出数列an , 从而求得bn , 利用分组求和法即可求得结果;(3)首先确定出数列{cn}的通项公式,利用放缩的思想将数列的每一项进行放缩,转化为特殊数列的求和问题达到证明不等式的目的.
,从而证得结论;(2)根据(1)求出数列an , 从而求得bn , 利用分组求和法即可求得结果;(3)首先确定出数列{cn}的通项公式,利用放缩的思想将数列的每一项进行放缩,转化为特殊数列的求和问题达到证明不等式的目的.
【考点精析】关于本题考查的等比关系的确定和数列的前n项和,需要了解等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;数列{an}的前n项和sn与通项an的关系 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知x=1是函数f(x)=![]() ax3-
ax3-![]() x2+(a+1)x+5的一个极值点.
x2+(a+1)x+5的一个极值点.
(1)求函数f(x)的解析式;
(2)若曲线y=f(x)与直线y=2x+m有三个交点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记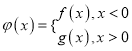 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(i)当![]() 时,若
时,若![]() 在
在![]() ,
, ![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ii)若在点![]() ,
, ![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(1)求证:PF⊥l;
(2)若PF=3,且双曲线的离心率e=![]() ,求该双曲线的方程.
,求该双曲线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用n种不同的颜色为下列两块广告牌着色,(如图甲、乙),要求在A,B,C,D四个区域中相邻(有公共边界)的区域不用同一颜色.
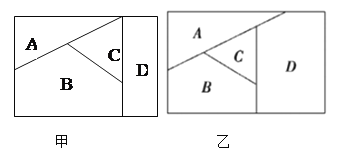
(1)若n=6,则为甲图着色时共有多少种不同的方法;
(2)若为乙图着色时共有120种不同方法,求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种水杯,每个水杯的原材料费、加工费分别为30元、m元(m为常数,且2≤m≤3),设每个水杯的出厂价为x元(35≤x≤41),根据市场调查,水杯的日销售量与ex(e为自然对数的底数)成反比例,已知每个水杯的出厂价为40元时,日销售量为10个.
(1)求该工厂的日利润y(元)与每个水杯的出厂价x(元)的函数关系式;
(2)当每个水杯的出厂价为多少元时,该工厂的日利润最大,并求日利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆E:
是椭圆E:![]() (a>b>0)上一点,离心率为
(a>b>0)上一点,离心率为![]() .
.
(1)求椭圆E的方程;
(2)设不过原点O的直线l与该椭圆E交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题: 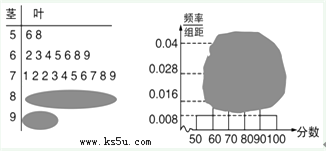
(1)求参加数学抽测的人数n、抽测成绩的中位数及分数分别在[80,90),[90,100]内的人数;
(2)若从分数在[80,100]内的学生中任选两人进行调研谈话,求恰好有一人分数在[90,100]内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com