
【题目】已知点![]() 是椭圆E:
是椭圆E:![]() (a>b>0)上一点,离心率为
(a>b>0)上一点,离心率为![]() .
.
(1)求椭圆E的方程;
(2)设不过原点O的直线l与该椭圆E交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
【答案】(1)![]() (2)(0,
(2)(0,![]() ).
).
【解析】试题分析:(1)根据离心率得a,b,c三者关系,再代入点![]() 可得a2=4,b2=3.(2)因为直线OP,PQ,OQ的斜率依次成等比数列,可得
可得a2=4,b2=3.(2)因为直线OP,PQ,OQ的斜率依次成等比数列,可得![]() ,再直线l的方程为y=kx+m(m≠0),联立直线方程与椭圆方程,利用韦达定理代入关系式得
,再直线l的方程为y=kx+m(m≠0),联立直线方程与椭圆方程,利用韦达定理代入关系式得![]() ,根据点到直线距离公式得高,根据弦长公式得底边边长,结合三角形面积公式得关于m函数关系式,最后利用基本不等式求最值,得取值范围
,根据点到直线距离公式得高,根据弦长公式得底边边长,结合三角形面积公式得关于m函数关系式,最后利用基本不等式求最值,得取值范围
试题解析:解:(1)由题意知,![]() =
=![]() ,
,
所以![]() =
=![]() ,a2=
,a2=![]() b2.
b2.
又![]() +
+![]() =1,解得a2=4,b2=3.
=1,解得a2=4,b2=3.
因此椭圆E的方程为![]()
(2)由题意可知,直线l的斜率存在且不为0,
故可设直线l的方程为y=kx+m(m≠0),
P(x1,y1),Q(x2,y2),
由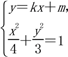 消去y得,
消去y得,
(3+4k2)x2+8kmx+4(m2-3)=0.
由题意知Δ=64k2m2-16(3+4k2)(m2-3)
=16(12k2-3m2+9)>0,
即4k2-m2+3>0.
又x1+x2=-![]() ,x1x2=
,x1x2=![]()
所以y1y2=(kx1+m)(kx2+m)
=k2x1x2+km(x1+x2)+m2=![]() .
.
因为直线OP,PQ,OQ的斜率依次成等比数列,
所以![]() ·
·![]() =
=![]() =k2,
=k2,
即(4k2-3)m2=0,
∵m≠0,∴k2=![]() .
.
由于直线OP,OQ的斜率存在,且Δ>0,
得0<m2<6,且m2≠3.
设d为点O到直线l的距离,
则S△OPQ=![]() d|PQ|
d|PQ|
=![]() ×
×![]()
![]() |x1-x2|
|x1-x2|
=![]() |m|
|m|![]()
又因为m2≠3,
所以S△OPQ=![]()
![]() <
<![]() ×
×![]() =
=![]() .
.
所以△OPQ面积的取值范围为(0,![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() ,an=
,an= ![]() (n≥2,n∈N).
(n≥2,n∈N).
(1)试判断数列 ![]() 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(2)设bn= ![]() ,求数列{bn}的前n项和Sn;
,求数列{bn}的前n项和Sn;
(3)设cn=ansin ![]() ,数列{cn}的前n项和为Tn . 求证:对任意的n∈N* , Tn<
,数列{cn}的前n项和为Tn . 求证:对任意的n∈N* , Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆E:
是椭圆E:![]() (a>b>0)上一点,离心率为
(a>b>0)上一点,离心率为![]() .
.
(1)求椭圆E的方程;
(2)设不过原点O的直线l与该椭圆E交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数{an}满a1=0,an+1=an+2n,那a2016的值是( )
A.2014×2015
B.2015×2016
C.2014×2016
D.2015×2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,![]() 为前
为前![]() 天两只老鼠打洞之和,则
天两只老鼠打洞之和,则![]() _________________尺.
_________________尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设(x1 , y1),(x2 , y2),…,(xn , yn),是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( ) 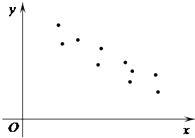
A.x和y正相关
B.x和y的相关系数为直线l的斜率
C.x和y的相关系数在﹣1到0之间
D.当n为偶数时,分布在l两侧的样本点的个数一定相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为![]() ,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
(Ⅰ)求袋中原有白球的个数:
(Ⅱ)求取球次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com