解:(1)因为f(x)是奇函数,所以f(-x)=-f(x),
所以log
a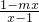
=log
a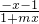
,…(2分)
即1-m
2x
2=1-x
2对一切x∈D都成立,…(3分)
所以m
2=1,m=±1,…(4分)
由于
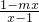
>0,所以m=-1…(5分)
所以f(x)=log
a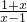
,D=(-∞,-1)∪(1,+∞)…(6分)
(2)当a>1时,f(x)=log
a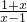
,任取x
1,x
2∈(1,+∞),x
1<x
2,…(7分)
则f(x
1)-f(x
2)=log
a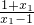
-log
a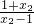
=log
a(
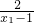
+1)-log
a(
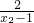
+1)…(9分)
由于x
1,x
2∈(1,+∞),x
1<x
2,所以
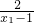
+1>
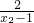
+1,得f(x
1)>f(x
2),…(10分)
【注】只要写出x
1,x
2∈(1,+∞),x
1<x
2,f(x
1)-f(x
2)=…=…,得出f(x
1)>f(x
2)即可.
即f(x)在(1,+∞)上单调递减…(11分)
同理可得,当0<a<1时,f(x)在(1,+∞)上单调递增 …(13分)
(3)因为x∈(r,a-2),定义域D=(-∞,-1)∪(1,+∞),
1°当r≥1时,则1≤r<a-2,即a>3,…(14分)
所以f(x)在(r,a-2)上为减函数,值域恰为(1,+∞),所以f(a-2)=1,…(15分)
即log
a
=log
a
=1,即

=a,…(16分)
所以a=2+

且r=1 …(18分)
2°当r<1时,则(r,a-2)?(-∞,-1),所以0<a<1
因为f(x)在(r,a-2)上为增函数,
所以f(r)=1,a-2=-1,
解得a=1与a>0且a≠1矛盾(舍) …(20分)
分析:(1)由函数f(x)是奇函数,可得出f(-x)=-f(x),由此方程恒成立,可得出参数m的方程,解出参数的值,再由对数的真数大于0得出x的不等式,解出函数的定义域即可;
(2)由于本题中参数a的取值范围未定,故应对它的取值范围分类讨论,判断函数的单调性再进行证明;
(3)由题设x∈(r,a-2)时,f(x)的值的范围恰为(1,+∞),可根据函数的单调性确定出两个参数a及r的方程,解方程得出两个参数的值.
点评:本题考察对数函数性质的综合运用,解答本题关键是熟练掌握对数的性质,函数单调性的证明方法,单调性的运用等结论,本题中第三小问是难点,第二问证明较繁琐,是本题的重点.本题考察了打理证明的能力,等价转化的能力以及转化的思想

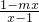 在定义域D上是奇函数,(其中a>0且a≠1).
在定义域D上是奇函数,(其中a>0且a≠1).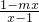 =loga
=loga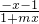 ,…(2分)
,…(2分)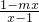 >0,所以m=-1…(5分)
>0,所以m=-1…(5分)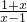 ,D=(-∞,-1)∪(1,+∞)…(6分)
,D=(-∞,-1)∪(1,+∞)…(6分)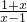 ,任取x1,x2∈(1,+∞),x1<x2,…(7分)
,任取x1,x2∈(1,+∞),x1<x2,…(7分)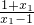 -loga
-loga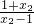 =loga(
=loga(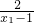 +1)-loga(
+1)-loga(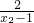 +1)…(9分)
+1)…(9分)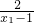 +1>
+1>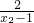 +1,得f(x1)>f(x2),…(10分)
+1,得f(x1)>f(x2),…(10分) =loga
=loga =1,即
=1,即 =a,…(16分)
=a,…(16分) 且r=1 …(18分)
且r=1 …(18分)

 中考解读考点精练系列答案
中考解读考点精练系列答案