已知数列{an},前n项和为Sn,若Sn+an=n2+3n-1,n∈N*.
(1)求a1,a2,a3,a4;
(2)是否存在常数p,q,使得数列{an+pn+q}为等比数列,若存在,求出数列{an}的通项公式;若不存在,请说明理由.
解:(1)∵S
n+a
n=n
2+3n-1,∴s
1+a
1=3,∴
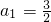
.
n=2时,(a
1+a
2)+a
2=2
2+3×2-1,∴
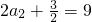
,∴
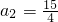
.
n=3时,(a
1+a
2+a
3)+a
3=3
2+3×3-1,∴

,∴

.
n=4时,(a
1+a
2+a
3+a
4)+a
4=4
2+3×4-1,∴

,∴
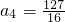
.
(2)∵S
n+a
n=n
2+3n-1,①
∴S
n+1+a
n+1=(n+1)
2+3(n+1)-1,②
②-①得S
n+1-S
n+a
n+1-a
n=2n+4,
∴2a
n+1-a
n=2n+4,∴

.
设
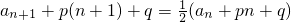
.
∴
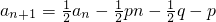
.
令
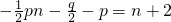
.∴
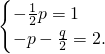
∴
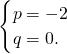
∴存在常数p=-2,q=0.使{a
n-2n}构成等比数列,首项

,公比为

,
∴
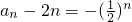
,∴

.
分析:(1)结合已知S
n+a
n=n
2+3n-1可把n=1,2,3,4,代入到递推公式中进行求解即可
(2)由已知S
n+a
n=n
2+3n-1可得,S
n+1+a
n+1=(n+1)
2+3(n+1)-1,考虑两式相减可得

.结合已知数列为等比数列可构造
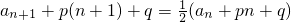
,利用待定系数法可求p,q,从而可求数列的通项公式
点评:本题主要考查了由数列的递推公式求解数列的项,及由数列的递推公式求解数列的通项公式,而等比数列的定义是解决等比数列最基本的方法.

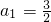 .
.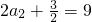 ,∴
,∴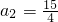 .
. ,∴
,∴ .
. ,∴
,∴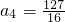 .
. .
.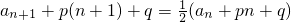 .
.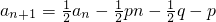 .
.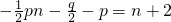 .∴
.∴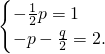 ∴
∴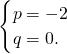
 ,公比为
,公比为 ,
,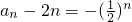 ,∴
,∴ .
. .结合已知数列为等比数列可构造
.结合已知数列为等比数列可构造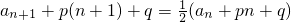 ,利用待定系数法可求p,q,从而可求数列的通项公式
,利用待定系数法可求p,q,从而可求数列的通项公式

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案