
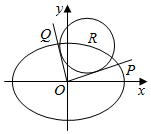
 如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆C:$\frac{x^2}{24}+\frac{y^2}{12}$=1上的一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,分别交椭圆于点P,Q.
如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆C:$\frac{x^2}{24}+\frac{y^2}{12}$=1上的一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,分别交椭圆于点P,Q.分析 (1)求得圆的半径r,由两直线垂直和相切的性质,可得|OR|=4,解方程可得圆心R的坐标,进而得到圆的方程;
(2)设出直线OP:y=k1x和OQ:y=k2x,由直线和圆相切的条件:d=r,化简整理,运用韦达定理,由R在椭圆上,即可得到k1•k2的值;
(3)讨论①当直线OP,OQ不落在坐标轴上时,设P(x1,y1),Q(x2,y2),运用点满足椭圆方程,由两点的距离公式,化简整理,即可得到定值36;②当直线OP,OQ落在坐标轴上时,显然有OP2+OQ2=36.
解答 解:(1)由圆R的方程知圆R的半径$r=2\sqrt{2}$,
因为直线OP,OQ互相垂直,且和圆R相切,
所以$|{OR}|=\sqrt{2}r=4$,即$x_0^2+y_0^2=16$①
又点R在椭圆C上,所以$\frac{x_0^2}{24}+\frac{y_0^2}{12}=1$②
联立①②,解得$\left\{{\begin{array}{l}{{x_0}=2\sqrt{2}}\\{{y_0}=2\sqrt{2}}\end{array}}\right.$,
所以,所求圆R的方程为${(x-2\sqrt{2})^2}+{(y-2\sqrt{2})^2}=8$;
(2)因为直线OP:y=k1x和OQ:y=k2x都与圆R相切,
所以$\frac{{|{{k_1}{x_0}-{y_0}}|}}{{\sqrt{1+k_1^2}}}=2\sqrt{2}$,$\frac{{|{{k_2}{x_0}-{y_0}}|}}{{\sqrt{1+k_2^2}}}=2\sqrt{2}$,
两边平方可得k1,k2为(x02-8)k2-2x0y0k+(y02-8)=0的两根,
可得${k_1}•{k_2}=\frac{y_0^2-8}{x_0^2-8}$,
因为点R(x0,y0)在椭圆C上,
所以$\frac{x_0^2}{24}+\frac{y_0^2}{12}=1$,即$y_0^2=12-\frac{1}{2}x_0^2$,
所以${k_1}{k_2}=\frac{{4-\frac{1}{2}x_0^2}}{x_0^2-8}=-\frac{1}{2}$;
(3)方法一①当直线OP,OQ不落在坐标轴上时,
设P(x1,y1),Q(x2,y2),
由(2)知2k1k2+1=0,
所以$\frac{{2{y_1}{y_2}}}{{{x_1}{x_2}}}+1=0$,故$y_1^2y_2^2=\frac{1}{4}x_1^2x_2^2$.
因为P(x1,y1),Q(x2,y2)在椭圆C上,
所以$\frac{x_1^2}{24}+\frac{y_1^2}{12}=1,\frac{x_2^2}{24}+\frac{y_2^2}{12}=1$,
即$y_1^2=12-\frac{1}{2}x_1^2,y_2^2=12-\frac{1}{2}x_2^2$,
所以$(12-\frac{1}{2}x_1^2)(12-\frac{1}{2}x_2^2)=\frac{1}{4}x_1^2x_2^2$,
整理得$x_1^2+x_2^2=24$,
所以$y_1^2+y_2^2=(12-\frac{1}{2}x_1^2)+(12-\frac{1}{2}x_2^2)=12$
所以$O{P^2}+O{Q^2}=x_1^2+y_1^2+x_2^2+y_2^2=(x_1^2+x_2^2)+(y_1^2+y_2^2)=36$.
方法(二)①当直线OP,OQ不落在坐标轴上时,
设P(x1,y1),Q(x2,y2),
联立$\left\{{\begin{array}{l}{y=kx}\\{\frac{x^2}{24}+\frac{y^2}{12}=1}\end{array}}\right.$,
解得$x_1^2=\frac{24}{1+2k_1^2},y_1^2=\frac{24k_1^2}{1+2k_1^2}$,
所以$x_1^2+y_1^2=\frac{24(1+k_1^2)}{1+2k_1^2}$,
同理,得$x_2^2+y_2^2=\frac{24(1+k_2^2)}{1+2k_2^2}$.
由(2)2k1k2+1=0,得${k_1}{k_2}=-\frac{1}{2}$,
所以$O{P^2}+O{Q^2}=x_1^2+y_1^2+x_2^2+y_2^2=\frac{24(1+k_1^2)}{1+2k_1^2}+\frac{24(1+k_2^2)}{1+2k_2^2}$
=$\frac{24(1+k_1^2)}{1+2k_1^2}+\frac{{24[{1+{{(-\frac{1}{{2{k_1}}})}^2}}]}}{{1+2{{(-\frac{1}{{2{k_1}}})}^2}}}=\frac{36+72k_1^2}{1+2k_1^2}=36$,
②当直线OP,OQ落在坐标轴上时,显然有OP2+OQ2=36.
综上:OP2+OQ2=36.
点评 本题考查椭圆方程的运用,以及直线和圆的位置关系:相切,考查点到直线的距离公式和直线方程的运用,考查分类讨论的思想方法,属于中档题.


科目:高中数学 来源: 题型:解答题
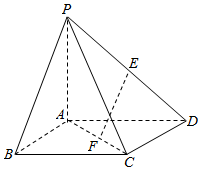 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PD,AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PD,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | $\frac{b}{a}>1$ | C. | a2<b2 | D. | ab<a+b-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2)(3) | B. | (1)(4)(5) | C. | (1)(2)(3) | D. | (2)(3)(4)(5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
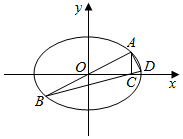 直线y=kx(k>0)与E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1交于A,B,C在x轴上,且AC⊥x轴,直线BC与E交于D,若AB⊥AD,则E的离心率为( )
直线y=kx(k>0)与E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1交于A,B,C在x轴上,且AC⊥x轴,直线BC与E交于D,若AB⊥AD,则E的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y-1=0 | B. | 2x-y-3=0 | C. | 2x+y-1=0 | D. | 2x+y-3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y | m | 3 | 5.5 | 7 |
| A. | 1 | B. | 0.85 | C. | 0.7 | D. | 0.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com