
分析 (Ⅰ)当a=1时,f(x)=x2+bx+c,结合|f(x)|≤1及绝对值三角不等式可证得:|1+c|≤1;
(Ⅱ)当b>2a>0时,$-\frac{b}{2a}<-1$,则f(x)在[-1,1]上递增且b>0,分类讨论满足|f(x)|≥b的x值,综合讨论结果可得答案.
解答 证明:(Ⅰ)当a=1时,f(x)=x2+bx+c,
∵|f(x)|≤1
∴|f(-1)|=|1-b+c|≤1,|f(1)|=|1+b+c|≤1,
∵|1-b+c+1+b+c|≤|1-b+c|+|1+b+c|≤2,
∴|2+2c|≤2
∴|1+c|≤1…(6分)
解:(Ⅱ)∵b>2a>0,
∴$-\frac{b}{2a}<-1$,则f(x)在[-1,1]上递增且b>0
∴f(x)∈[a-b+c,a+b+c]…(9分)
①当a+c>0时,a+b+c>b>0…(11分)
此时有|f(1)|≥b即存在x=1,使得|f(x)|≥b成立
②当a+c<0时,a-b+c<-b<0…(13分)
此时有|f(-1)|≥b即存在x=-1使得|f(x)|≥b成立
③当a+c=0时,f(x)∈[-b,b],存在x使得|f(x)|≥b成立
∴存在x=±1使得|f(x)|≥b成立…(15分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
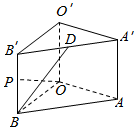 如图所示,在直三棱柱ABO-A′B′O′中,OO′=4,OA=4,OB=3,∠AOB=90°,D是线段A′B′的中点,P是侧棱BB′上的一点,若OP⊥BD,求OP与底面AOB所成角的正切值.
如图所示,在直三棱柱ABO-A′B′O′中,OO′=4,OA=4,OB=3,∠AOB=90°,D是线段A′B′的中点,P是侧棱BB′上的一点,若OP⊥BD,求OP与底面AOB所成角的正切值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 2π | C. | 3π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
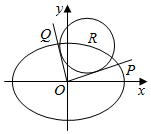 如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆C:$\frac{x^2}{24}+\frac{y^2}{12}$=1上的一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,分别交椭圆于点P,Q.
如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆C:$\frac{x^2}{24}+\frac{y^2}{12}$=1上的一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,分别交椭圆于点P,Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 数学成绩分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) | [100,110) | [110,120] |
| 频数 | 1 | 2 | 3 | 7 | 6 | 5 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16($π-\sqrt{3}$) | B. | 16($π-\sqrt{2}$) | C. | 8(2$π-3\sqrt{2}$) | D. | 8(2$π-\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一只转盘,均匀标有8个数,现转动转盘,则转盘停止转动时,指针向奇数的概率是( )
如图,一只转盘,均匀标有8个数,现转动转盘,则转盘停止转动时,指针向奇数的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com