解:(Ⅰ)x,y∈R,有f(x+y)=f(x)f(y).
当x<0时,f(x)>1
令x=-1,y=0则f(-1)=f(-1)f(0)
∵f(-1)>1∴f(0)=1…(3分)
若x>0,则f(x-x)=f(0)=f(x)f(-x)故f(x)=
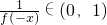
,
任取x
1<x
2 f(x
2)=f(x
1+x
2-x
1)=f(x
1)f(x
2-x
1),
∵x
2-x
1>0,∴0<f(x
2-x
1)<1,
∴f(x
1)>f(x
2).
故f(x)在R上减函数…(6分)
(Ⅱ)f(a
n+1)=
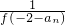
=f(2+a
n)(n∈N
*)
由f(x)单调性得:a
n+1=a
n+2
故{a
n}是等差数列,a
n=a
1+2(n-1)…(8分)
∵存在t,s∈N
*,使得(t,a
s)和(s,a
t)都在y=kx-1上,
∴a
s=kt-1,①a
t=ks-1,②
①-②得a
s-a
t=k(t-s).
又a
s=a
1+2(s-1),a
t=a
1+2(t-1),故a
s-a
t=-2(t-s),
∵s≠t,∴k=-2
①+②,得a
s+a
t=-2(t+s)-2,
又a
s+a
t=a
1+2(s-1)+a
1+2(t-1)
=2a
1+2(s+t)-4,
∴2a
1+2(s+t)-4=-2(t+s)-2
∴a
1=-2(t+s)+1<0,∴a
n=-2(t+s)-1+2n…(10分)
即数列{a
n}是首项为负奇数,公差为2,故数列{a
n}是递增等差数列,各项全为奇数,
又f(0)=1
∴一定存在一个自然数M,使
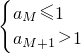
∴
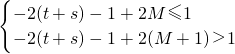
解得t+s<M≤t+s+1.…(12分)
∵M∈N,
∴M=t+s+1,
∴存在自然数M=t+s+1,使得当n>M时,a
n>f(0)恒成立.…(14分)
分析:(Ⅰ)x,y∈R,有f(x+y)=f(x)f(y).当x<0时,令x=-1,y=0以及f(-1)>1,推出f(0)=1,利用单调性的定义任取x
1<x
2 推出 f(x
2)=f(x
1+x
2-x
1)=f(x
1)f(x
2-x
1),得到f(x)在R上减函数.
(Ⅱ)通过函数的单调性,得到a
n+1=a
n+2,点(t,a
s)、(s,a
t)都在直线y=kx-1上,推出a
s-a
t=-2(t-s),
确定a
n=-2(t+s)-1+2n,通过当n>M时,a
n>f(0)恒成立,推出
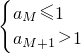
然后求出M的最小值.
点评:本题考查数列与函数的关系,数列的判断,函数的单调性的应用,考查转化思想,分析问题解决问题的能力,难度较大.

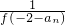 (n∈N*)
(n∈N*)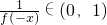 ,
,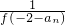 =f(2+an)(n∈N*)
=f(2+an)(n∈N*)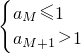
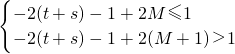
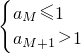 然后求出M的最小值.
然后求出M的最小值.

 )与b=f(
)与b=f( )的大小关系为________.
)的大小关系为________. )与b=f(
)与b=f( )的大小关系为 .
)的大小关系为 . )与b=f(
)与b=f( )的大小关系为( ).
)的大小关系为( ).