
分析 求得A,B,F点坐标,根据中点坐标公式,代入求得M坐标,$\overrightarrow{MA}$=(-$\frac{a}{2}$,-$\frac{b}{2}$),$\overrightarrow{BA}$=(-a,-b),则$\overrightarrow{BA}$•$\overrightarrow{MF}$+${\overrightarrow{BF}}^{2}$<0,根据向量的数量积的坐标运算,利用离心率公式,即可求得椭圆离心率的取值范围.
解答 解:由题意,A(-a,0),B(0,b),F(c,0),则M(-$\frac{a}{2}$,$\frac{b}{2}$),
$\overrightarrow{MA}$=(-$\frac{a}{2}$,-$\frac{b}{2}$),$\overrightarrow{BA}$=(-a,-b),
∵2$\overrightarrow{MA}$•$\overrightarrow{MF}$+$\overrightarrow{BF}$2<0,
$\overrightarrow{BA}$•$\overrightarrow{MF}$+${\overrightarrow{BF}}^{2}$<0
∴(-a,-b)(c+$\frac{a}{2}$,-$\frac{b}{2}$)+b2+c2<0,
∴-ac-$\frac{{a}^{2}}{2}$+$\frac{{a}^{2}-{c}^{2}}{2}$+a2<0,整理得:c2+2ac-2a2>0,
由椭圆的离心率e=$\frac{c}{a}$,两边同除以a2,
∴e2+2e-2>0
∴e<-1-$\sqrt{3}$或e>$\sqrt{3}$-1,
∵0<e<1,
∴$\sqrt{3}$-1<e<1,
故答案为:($\sqrt{3}$-1,1).
点评 本题考查椭圆的简单几何性质,考查向量数量积的坐标运算,一元二次不等式的解法,考查计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
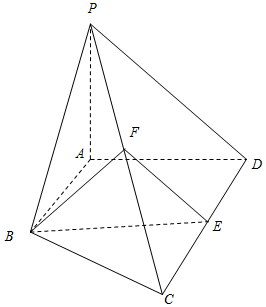 如图,在四棱锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
如图,在四棱锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg(x2+$\frac{1}{4}$)>lgx(x>0) | B. | sin x+$\frac{1}{sinx}$≥2(x≠$\frac{kπ}{2}$,k∈Z) | ||
| C. | x2+1≥2|x|(x∈R) | D. | $\frac{1}{{x}^{2}+1}$>1(x∈R) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}({2}^{n}-1)$ | B. | $\frac{5}{18}({3}^{n}-1)$ | C. | $5•{2}^{n-1}-\frac{5}{4}$ | D. | $5•{2}^{n-2}-\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
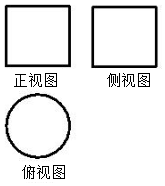
| A. | 6π | B. | $8\sqrt{2}$π | C. | $4+4\sqrt{2}$π | D. | $8+4\sqrt{2}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com