
分析 (1)Sn=2an-n,(n∈N*),可得n=1时,a1=2a1-1,解得a1.n≥2时,an=Sn-Sn-1,可得an+1=2(an-1+1),利用等比数列的定义及其通项公式即可得出.
(2)bn=(2n+1)an+2n+1=(2n+1)•2n,利用“错位相减法”与等比数列的求和公式即可得出.
(3)cn=3n+(-1)n-1λ•(an+1)=3n+λ(-1)n-12n,假设存在整数λ,使得对任意n∈N*,都有cn+1>cn,即3n+1+λ(-1)n•2n+1>3n+λ(-1)n-12n,对n分类讨论即可得出.
解答 (1)证明:∵Sn=2an-n,(n∈N*),∴n=1时,a1=2a1-1,解得a1=1.
n≥2时,an=Sn-Sn-1=2an-n-(2an-1-n+1),可得an=2an-1+1,变形为an+1=2(an-1+1),
∴{an+1}是等比数列,首项为2,公比为2.
∴an+1=2n,即an=2n-1.
(2)解:bn=(2n+1)an+2n+1=(2n+1)•2n,
∴数列{bn}的前n项和为Tn=3×2+5×22+…+(2n+1)•2n,
2Tn=3×22+5×23+…+(2n-1)•2n+(2n+1)•2n+1,
∴-Tn=3×2+2(22+23+…+2n)-(2n+1)•2n+1=2+$\frac{4×({2}^{n}-1)}{2-1}$-(2n+1)•2n+1,
解得Tn=2+(2n-1)•2n+1.
(3)解:cn=3n+(-1)n-1λ•(an+1)=3n+λ(-1)n-12n,
假设存在整数λ,使得对任意n∈N*,都有cn+1>cn,
则3n+1+λ(-1)n•2n+1>3n+λ(-1)n-12n,
n=2k(k∈N*)时,λ>$\frac{{3}^{n}-{3}^{n+1}}{{2}^{n}+{2}^{n+1}}$=$-(\frac{3}{2})^{n-1}$,∴λ>-$(\frac{3}{2})^{2-1}$=-$\frac{3}{2}$.
n=2k-1(k∈N*)时,∴λ$<(\frac{3}{2})^{n-1}$.∴$λ<\frac{3}{2}$.
综上可得:$-\frac{3}{2}<λ<\frac{3}{2}$.
因此存在整数λ=-1,0,1,使得对任意n∈N*,都有cn+1>cn.
点评 本题考查了“错位相减法”、等比数列的定义通项公式与求和公式、数列的单调性、数列递推关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | $10+2\sqrt{3}$ | C. | $10+2\sqrt{5}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
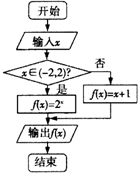
| A. | [0,log23] | B. | [-2,2] | C. | [0,log23]∪{2} | D. | [-2,log23]∪{2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com