练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．若y=alnx+bx2+x在x=1和x=2处有极值，则a=-$\frac{2}{3}$，b=-$\frac{1}{6}$．

    分析 函数的极值点处的导数值为0，列出方程，求出a，b的值．

    解答 解：f′（x）=$\frac{a}{x}$+2bx+1，
    由已知得：$\left\{\begin{array}{l}{f′（1）=0}\\{f′（2）=0}\end{array}\right.$⇒$\left\{\begin{array}{l}{a+2b+1=0}\\{\frac{1}{2}a+4b+1=0}\end{array}\right.$，
    ∴a=-$\frac{2}{3}$，b=-$\frac{1}{6}$，
    故答案为：-$\frac{2}{3}$，-$\frac{1}{6}$．

    点评 本题考查了导数的应用，考查函数极值的意义，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．若$tan（{α+\frac{π}{4}}）=-3$，则cos2α+2sin2α=（　　）
    A．$\frac{9}{5}$B．1C．$-\frac{3}{5}$D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

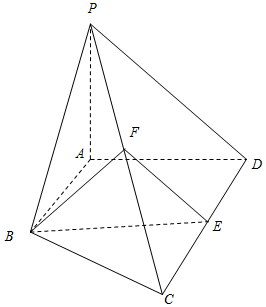    7．如图，在四棱锥P-ABCD中，AB∥CD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．
    求证：（1）PA⊥底面ABCD；（2）平面BEF∥平面PAD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知数列{an}的前n项和为Sn，且满足Sn=2an-n，（n∈N*）
    （1）证明：{an+1}是等比数列；并求数列{an}的通项公式；
    （2）若bn=（2n+1）an+2n+1，求数列{bn}的前n项和为Tn；
    （3）若cn=3n+（-1）n-1λ•（an+1）（λ为非零常数，n∈N*），问是否存在整数λ，使得对任意n∈N*，都有cn+1＞cn？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．下列不等式一定成立的是（　　）
    A．lg（x2+$\frac{1}{4}$）＞lgx（x＞0）B．sin x+$\frac{1}{sinx}$≥2（x≠$\frac{kπ}{2}$，k∈Z）
    C．x2+1≥2|x|（x∈R）D．$\frac{1}{{x}^{2}+1}$＞1（x∈R）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．在△ABC中，A=60°，a=6$\sqrt{3}$，则$\frac{a+b+c}{sinA+sinB+sinC}$=12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知正项等比数列{an}的前n项和为Sn，已知S4-S1=7a2，a3=5，则Sn=（　　）
    A．$\frac{5}{2}（{2}^{n}-1）$B．$\frac{5}{18}（{3}^{n}-1）$C．$5•{2}^{n-1}-\frac{5}{4}$D．$5•{2}^{n-2}-\frac{5}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若函数f（x）=x2+bx+c的图象的顶点在第四象限，则函数f′（x）的图象是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．近年来，某地区为促进本地区发展，通过不断整合地区资源、优化投资环境、提供投资政策扶持等措施，吸引外来投资，效果明显．该地区引进外来资金情况如表：
    年份20122013201420152016
    时间代号t12345
    外来资金y（百亿元）567810
    （Ⅰ）求y关于t的回归直线方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$；
    （Ⅱ）根据所求回归直线方程预测该地区2017年（t=6）引进外来资金情况．
    参考公式：回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$中斜率和截距的最小二乘估计公式分别为：
    $\widehat{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$t．

    查看答案和解析>>

    同步练习册答案