
分析 (1)由x2-2x-3>0 可得(x-3)(x+1)>0,可得(x-3)>0且(x+1)>0或(x-3)<0且(x+1)<0,可得答案.
(2)根据分式不等式$\frac{x-2}{x-1}$≤0等价于(x-2)(x-1)≤0且(x-1)≠0可得答案.
解答 解:(1)x2-2x-3>0 可得(x-3)(x+1)>0,可得(x-3)>0且(x+1)>0或(x-3)<0且(x+1)<0,
解得:x>3或x<-1.
故得不等式的解集为:{x|x>3或x<-1}
(2)(2)$\frac{x-2}{x-1}$≤0等价于(x-2)(x-1)≤0且(x-1)≠0,
解得:1<x≤2.
故得不等式的解集为:{x|1<x≤2}.
点评 二次不等式,分式不等式的解法,体现了等价转化数学思想,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | $\root{3}{4}$<a<2 | B. | 1<a<2 | C. | $\root{3}{4}$<a<$\root{6}{9}$ | D. | 1<a<$\root{3}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Sn<an | B. | Sn≤an | C. | Sn>an | D. | 大小不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
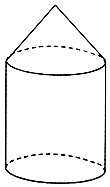 如图,某粮仓是由圆柱和圆锥构成(粮仓的底部位于地面上),圆柱的底面直径与高都等于h米,圆锥的高为$\frac{1}{2}$h米.
如图,某粮仓是由圆柱和圆锥构成(粮仓的底部位于地面上),圆柱的底面直径与高都等于h米,圆锥的高为$\frac{1}{2}$h米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{5}$ | B. | 1 | C. | $-\frac{3}{5}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com