解:(Ⅰ)∵直线l与函数f(x)的图象相切,且切点的横坐标为1.
∴切点坐标为P(1,ln1),即P(1,0)
求得f′(x)=

,所以切线斜率为k=f′(1)=1
∴直线l的方程为y=x-1
又∵直线l与函数y=g(x)的图象相切,设切点为Q(x
0,x
0-1)
∴
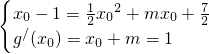
?m=-2或4
∵m<0∴x
0=-2
故所求直线方程为y=x-1,m的值是-2
(Ⅱ)由(I)得g′(x)=x-2
∴h(x)=f(x+1)-g′(x)=ln(x+1)-x+2
求导:h′(x)=

(x>-1)
当x∈(-1,0)时,h′(x)>0,函数h(x)是增函数;
当x∈(0,+∞)时,h′(x)<0,函数h(x)是减函数
∴函数h(x)在x=0时有极大值,并且这个极大值是最大值
故函数h(x)的最大值为h(0)=2;
(Ⅲ)为了比较:a+2af(a+b)与b+2af(2a)的大小,进行作差:
[a+2af(a+b)]-[b+2af(2a)]=a-b+2a[f(a+b)-f(2a)]=a-b+2aln(
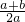
)
∵0<b<a
∴设a-b=t,(t>0),得a=b+t
可得a-b+2aln(
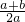
)=t+2(b+t)ln[

]
再记
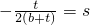
,(-1<s<0),
F(s)=ln(1+s)-s?F′(s)=

>0
∴F(s)在(-1,0)是增函数,F(s)<F(0)=0
∴t+2(b+t)ln[

]<t+2(b+t)
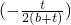
=t-t=0
即a-b+2aln(
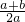
)<0
∴a+2af(a+b)<b+2af(2a)
分析:(Ⅰ)根据直线l与函数f(x)的图象切点的横坐标为1,得到切点P(1,0),再求出斜率k=f′(1),用点斜式方程可求直线l的方程.再设直线l与函数y=g(x)图象切点为Q(x
0,x
0-1),根据两曲线的公共点和导数的几何意义联列方程组,解之可得m的值;
(Ⅱ)由(I)的结果,得h(x)=ln(x+1)-x+2,通过求导数、讨论h′(x)的符号,得到函数h(x)在区间(-1,0)上是增函数,在区间(0,+∞)上是减函数,从而得出函数h(x)的最大值是h(0)=2;
(III)先作差:[a+2af(a+b)]-[b+2af(2a)]=a-b+2aln(
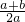
),然后记a-b=t,(t>0),得a=b+t,将所得的差化为以b和t为单位的式子,再记
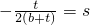
,F(s)=ln(1+s)-s,通过讨论其单调性得ln(1+s)<s,最后将此不等式还原为以b和t为单位的式子,运用不等式的性质进行放缩,可得a-b+2aln(
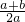
)<0,最终得到a+2af(a+b)<b+2af(2a).
点评:本题考查了利用导数研究曲线上某点切线方程、导数在最大值、最小值问题中的应用以及不等式与函数相综合等知识点,属于难题.解题时应该注意转化化归思想与不等式放缩等技巧的运用.

 x2+mx+
x2+mx+ (m<0),直线l与函数f(x)、g(x)的图象都相切,且与函数f(x)的图象的切点的横坐标为1.
(m<0),直线l与函数f(x)、g(x)的图象都相切,且与函数f(x)的图象的切点的横坐标为1. ,所以切线斜率为k=f′(1)=1
,所以切线斜率为k=f′(1)=1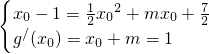 ?m=-2或4
?m=-2或4 (x>-1)
(x>-1)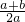 )
)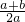 )=t+2(b+t)ln[
)=t+2(b+t)ln[ ]
]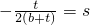 ,(-1<s<0),
,(-1<s<0), >0
>0 ]<t+2(b+t)
]<t+2(b+t)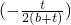 =t-t=0
=t-t=0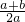 )<0
)<0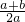 ),然后记a-b=t,(t>0),得a=b+t,将所得的差化为以b和t为单位的式子,再记
),然后记a-b=t,(t>0),得a=b+t,将所得的差化为以b和t为单位的式子,再记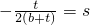 ,F(s)=ln(1+s)-s,通过讨论其单调性得ln(1+s)<s,最后将此不等式还原为以b和t为单位的式子,运用不等式的性质进行放缩,可得a-b+2aln(
,F(s)=ln(1+s)-s,通过讨论其单调性得ln(1+s)<s,最后将此不等式还原为以b和t为单位的式子,运用不等式的性质进行放缩,可得a-b+2aln(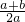 )<0,最终得到a+2af(a+b)<b+2af(2a).
)<0,最终得到a+2af(a+b)<b+2af(2a).
