解:(Ⅰ)设点M(x,y),由题意得点F(

,0),

,化简可得 x
2+y
2=2,
故曲线C的方程为 x
2+y
2=2,表示以原点为圆心,以

为半径的圆.
(Ⅱ)∵点
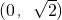
是圆和y轴的交点,经过点
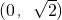
且斜率为k的直线l与曲线C有两个不同的交点P和Q,
∴线l与曲线C不能相切,∴k≠0.
(Ⅲ) 把直线l的方程 y-

=k(x-0)代入曲线C的方程 x
2+y
2=2 得,(1+k
2)x
2+2

kx=0.
设P(x
1,y
1 ),Q(x
2,y
2),则 x
1+x
2=-

,x
1•x
2=0.
∴
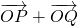
=(x
1+x
2,kx
1+

+kx
2+

)=(
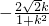
,
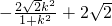
).
由B(0,

),A
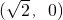
,∴

=(-

,

).∵向量
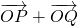
与

共线,
∴
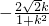
•

-(-

)(
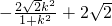
)=0,
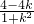
=0,∴k=1.
即存在常数 k=1 满足题中的条件.
分析:(Ⅰ)设点M(x,y),由题意得点F(

,0),

,化简可得曲线C的方程.
(Ⅱ) 直线l经过圆和y轴的交点(0,

),直线l与曲线C有两个不同的交点,故直线l与曲线C不能相切,k≠0.
(Ⅲ) 把直线l的方程代入曲线C的方程,利用根与系数的关系,求得
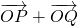
的坐标,再利用
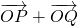
与

共线,求出 k值.
点评:本题考查直接利用条件求点的轨迹方程的方法,向量坐标形式的运算,两个向量共线的性质,准确计算是解题的难点.

 ,0)关于原点O对称,M是动点,且直线EM与FM的斜率之积等于
,0)关于原点O对称,M是动点,且直线EM与FM的斜率之积等于 .设点M的轨迹为曲线C,经过点
.设点M的轨迹为曲线C,经过点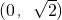 且斜率为k的直线l与曲线C有两个不同的交点P和Q.
且斜率为k的直线l与曲线C有两个不同的交点P和Q.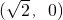 ,曲线C与y轴正半轴的交点为B,是否存在常数k,使得向量
,曲线C与y轴正半轴的交点为B,是否存在常数k,使得向量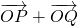 与
与 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由. ,0),
,0), ,化简可得 x2+y2=2,
,化简可得 x2+y2=2, 为半径的圆.
为半径的圆.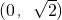 是圆和y轴的交点,经过点
是圆和y轴的交点,经过点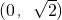 且斜率为k的直线l与曲线C有两个不同的交点P和Q,
且斜率为k的直线l与曲线C有两个不同的交点P和Q, =k(x-0)代入曲线C的方程 x2+y2=2 得,(1+k2)x2+2
=k(x-0)代入曲线C的方程 x2+y2=2 得,(1+k2)x2+2 kx=0.
kx=0. ,x1•x2=0.
,x1•x2=0.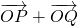 =(x1+x2,kx1+
=(x1+x2,kx1+ +kx2+
+kx2+ )=(
)=(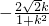 ,
,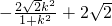 ).
). ),A
),A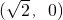 ,∴
,∴ =(-
=(- ,
, ).∵向量
).∵向量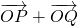 与
与 共线,
共线,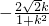 •
• -(-
-(- )(
)(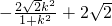 )=0,
)=0,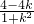 =0,∴k=1.
=0,∴k=1. ,0),
,0), ,化简可得曲线C的方程.
,化简可得曲线C的方程. ),直线l与曲线C有两个不同的交点,故直线l与曲线C不能相切,k≠0.
),直线l与曲线C有两个不同的交点,故直线l与曲线C不能相切,k≠0.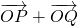 的坐标,再利用
的坐标,再利用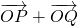 与
与 共线,求出 k值.
共线,求出 k值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.