精英家教网 > 高中数学 > 题目详情

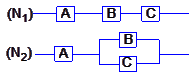
如图，用A、B、C三类不同的元件连接成两个系统N₁、N₂，当元件A、B、C都正常工作时，系统N₁正常工作；当元件A正常工作且元件B、C至少有一个正常工作时，系统N₂正常工作, 已知元件A、B、C正常工作的概率依次为0.80,0.90,0.90，分别求系统N₁，N₂正常工作的概率P₁、P₂.

(1) 系统N₁正常工作的概率为0.648 (2) 系统N₂正常工作的概率为0.792

解析:

记元件A、B、C正常工作的事件分别为A、B、C，

由已知条件P(A)=0.80, P(B)=0.90,P(C)=0.90.

(1)因为事件A、B、C是相互独立的，所以，系统N₁正常工作的概率P₁=P(A·B·C)=P(A)P(B)P(C)=0.648,故系统N₁正常工作的概率为0.648.

(2)系统N₂正常工作的概率P₂=P(A)·［1－P()］

=P(A)·［1－P()P()］

=0.80×［1－(1－0 .90)(1－0.90)］=0.792

故系统N₂正常工作的概率为0.792.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

8、如图，用A，B，C三个不同的元件连接成一个系统N．当元件A正常工作且元件B、C至少有一个正常工作时，系统N正常工作．已知元件A，B，C正常工作的概率依次为0.8，0.85，0.9，则系统N能正常工作的概率等于

0.788

．

查看答案和解析>>

科目：高中数学 来源： 题型：

如图所示，直三棱柱ABC-A₁B₁C₁中，AB⊥AC，D，E分别为AA₁，B₁C的中点，若记

，

，则

（用

，

表示）．

查看答案和解析>>

科目：高中数学 来源： 题型：

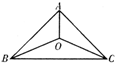三个城市分别位于A，B，C三点处（如图），且AB=AC=20

km，BC=40km．今计划合建一个货运中转站，为同时方便三个城市，准备建在与B、C等距离的O点处，并修建道路OA，OB，OC．记修建的道路的总长度为ykm．
（Ⅰ）设OA=x（km），或OB=x（km），或点O到BC的距离为x（km），或∠CBO=x（rad）．请你选择用其中的某个x，将y表示为x的函数；
（Ⅱ）由（Ⅰ）中建立的函数关系，确定货运中转站的位置，使修建的道路的总长度最短．

查看答案和解析>>

科目：高中数学 来源： 题型：