Question

14．设abc＞0，二次函数f（x）=ax²+bx+c的图象可能是下列图形中的①（填序号）．

Answer 1

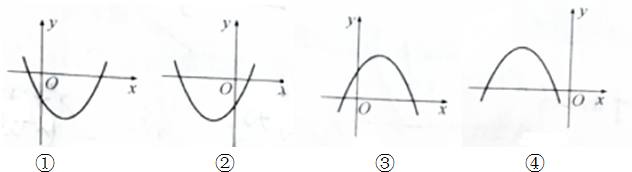
分析 当a＞0时，二次函数开口向上，判断①②中c的符号，再确定b的符号，判断①②的正误；当a＜0时，同样的方法判断③④的正误．

解答 解：当a＞0时，因为abc＞0，所以b、c同号，由①②两图中可知c＜0，
故b＜0，∴-$\frac{b}{2a}$＞0，即函数对称轴在y轴右侧，②不正确，①符合题意．
显然a＜0时，开口向下，因为abc＞0，所以b、c异号，
对于③，c＞0，对称轴-$\frac{b}{2a}$＜0，不正确．
对④，由图象可知c＜0，则b＞0，对称轴-$\frac{b}{2a}$＞0，不正确．
故答案为：①．

点评 根据二次函数图象开口向上或向下，分a＞0或a＜0两种情况分类考虑．另外还要注意c值是抛物线与y轴交点的纵坐标，还要注意对称轴的位置或定点坐标的位置等．是常考题．