
【题目】某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为![]() ,高为
,高为![]() ,圆锥的母线长为
,圆锥的母线长为![]() .
.
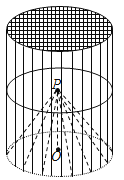
(1)求这种“笼具”的体积(结果精确到0.1![]() );
);
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面上,给定非零向量![]() ,对任意向量
,对任意向量![]() ,定义
,定义![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() ,证明:若位置向量
,证明:若位置向量![]() 的终点在直线
的终点在直线![]() 上,则位置向量
上,则位置向量![]() 的终点也在一条直线上;
的终点也在一条直线上;
(3)已知存在单位向量![]() ,当位置向量
,当位置向量![]() 的终点在抛物线
的终点在抛物线![]() :
:![]() 上时,位置向量
上时,位置向量![]() 终点总在抛物线
终点总在抛物线![]() :
:![]() 上,曲线
上,曲线![]() 和
和![]() 关于直线
关于直线![]() 对称,问直线
对称,问直线![]() 与向量
与向量![]() 满足什么关系?
满足什么关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,直线
时,直线![]() 与
与![]() 相切,求
相切,求![]() 的值;
的值;
(2)若函数![]() 在
在![]() 内有且只有一个零点,求此时函数
内有且只有一个零点,求此时函数![]() 的单调区间;
的单调区间;
(3)当![]() 时,若函数
时,若函数![]() 在
在![]() 上的最大值和最小值的和为1,求实数
上的最大值和最小值的和为1,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子科技公司由于产品采用最新技术,销售额不断增长,最近![]() 个季度的销售额数据统计如下表(其中
个季度的销售额数据统计如下表(其中![]() 表示
表示![]() 年第一季度,以此类推):
年第一季度,以此类推):
季度 |
|
|
|
|
|
季度编号x |
|
|
|
|
|
销售额y(百万元) |
|
|
|
|
|
(1)公司市场部从中任选![]() 个季度的数据进行对比分析,求这
个季度的数据进行对比分析,求这![]() 个季度的销售额都超过
个季度的销售额都超过![]() 千万元的概率;
千万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 的销售额.
的销售额.
附:线性回归方程:![]() 其中
其中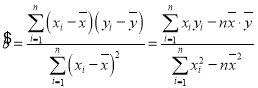 ,
,![]()
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左焦点为
的左焦点为![]() ,点A的坐标为(0,1),点P为双曲线右支上的动点,且△APF1周长的最小值为6,则双曲线的离心率为( )
,点A的坐标为(0,1),点P为双曲线右支上的动点,且△APF1周长的最小值为6,则双曲线的离心率为( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,该椭圆经过点
,该椭圆经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 是圆
是圆![]() 上任意一点,由
上任意一点,由![]() 引椭圆
引椭圆![]() 的两条切线
的两条切线![]() ,
,![]() ,当两条切线的斜率都存在时,证明:两条切线斜率的积为定值.
,当两条切线的斜率都存在时,证明:两条切线斜率的积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com