
【题目】设函数f(x)= ![]() (其中常数a>0,且a≠1).
(其中常数a>0,且a≠1).
(1)当a=10时,解关于x的方程f(x)=m(其中常数m>2 ![]() );
);
(2)若函数f(x)在(﹣∞,2]上的最小值是一个与a无关的常数,求实数a的取值范围.
【答案】
(1)解:f(x)= 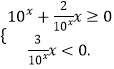
①当x<0时,f(x)= ![]() >3.因为m>2
>3.因为m>2 ![]() .
.
则当2 ![]() <m≤3时,方程f(x)=m无解;
<m≤3时,方程f(x)=m无解;
当m>3,由10x= ![]() ,得x=lg
,得x=lg ![]() .
.
②当x≥0时,10x≥1.由f(x)=m得10x+ ![]() =m,
=m,
∴(10x)2﹣m10x+2=0.
因为m>2 ![]() ,判别式△=m2﹣8>0,解得10x=
,判别式△=m2﹣8>0,解得10x= ![]() .
.
因为m>2 ![]() ,所以
,所以 ![]() >
> ![]() >1.
>1.
所以由10x= ![]() ,解得x=lg
,解得x=lg ![]() .
.
令 ![]() =1,得m=3.
=1,得m=3.
所以当m>3时, ![]() =
= ![]() <
< ![]() =1,
=1,
当2 ![]() <m≤3时,
<m≤3时, ![]() =
= ![]() >
> ![]() =1,解得x=lg
=1,解得x=lg ![]() .
.
综上,当m>3时,方程f(x)=m有两解x=lg ![]() 和x=lg
和x=lg ![]() ;
;
当2 ![]() <m≤3时,方程f(x)=m有两解x=lg
<m≤3时,方程f(x)=m有两解x=lg ![]() .
.
(2)解:①若0<a<1,
当x<0时,0<f(x)= ![]() <3;
<3;
当0≤x≤2时,f(x)=ax+ ![]() .
.
令t=ax,则t∈[a2,1],g(t)=t+ ![]() 在[a2,1]上单调递减,
在[a2,1]上单调递减,
所以当t=1,即x=0时f(x)取得最小值为3.
当t=a2时,f(x)取得最大值为 ![]() .
.
此时f(x)在(﹣∞,2]上的值域是(0, ![]() ],没有最小值.
],没有最小值.
②若a>1,
当x<0时,f(x)= ![]() >3;
>3;
当0≤x≤2时f(x)=ax+ ![]() .
.
令t=ax,g(t)=t+ ![]() ,则t∈[1,a2].
,则t∈[1,a2].
①若a2≤ ![]() ,g(t)=t+
,g(t)=t+ ![]() 在[1,a2]上单调递减,
在[1,a2]上单调递减,
所以当t=a2即x=2时f(x)取最小值a2+ ![]() ,最小值与a有关;
,最小值与a有关;
②a2> ![]() ,g(t)=t+
,g(t)=t+ ![]() 在[1,
在[1, ![]() ]上单调递减,在[
]上单调递减,在[ ![]() ,a2]上单调递增,
,a2]上单调递增,
所以当t= ![]() 即x=loga
即x=loga ![]() 时f(x)取最小值2
时f(x)取最小值2 ![]() ,最小值与a无关.
,最小值与a无关.
综上所述,当a≥ ![]() 时,f(x)在(﹣∞,2]上的最小值与a无关.
时,f(x)在(﹣∞,2]上的最小值与a无关.
【解析】(1)当a=10时,脱掉绝对值,写出f(x)的分段函数,根据分段函数在相应的区间所对应的解析式进行求解,(2)根据题意有![]() ,对a进行分类讨论,①a>1时,②0<a<1时,两种情况分析,每种情况下根据绝对值,再按照x≥0时,和-2≤x<0两种情况讨论,最后可得结论.
,对a进行分类讨论,①a>1时,②0<a<1时,两种情况分析,每种情况下根据绝对值,再按照x≥0时,和-2≤x<0两种情况讨论,最后可得结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. 
(1)求证:OE⊥FC:
(2)若 ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b是两个实数,给出下列条件:
①a+b>1;②a+b=2;③a+b>2;④a2+b2>2;⑤ab>1.
其中能推出:“a,b中至少有一个大于1”的条件是 .(填序号,只有一个正确选项)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为(0,+∞)的函数f(x)满足:
①x>1时,f(x)<0;
②f( ![]() )=1;
)=1;
③对任意的正实数x,y,都有f(xy)=f(x)+f(y).
(1)求证:f( ![]() )=﹣f(x);
)=﹣f(x);
(2)求证:f(x)在定义域内为减函数;
(3)求满足不等式f(log0.5m+3)+f(2log0.5m﹣1)≥﹣2的m集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 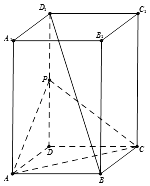
(1)求证:直线BD1∥平面PAC
(2)求证:平面PAC⊥平面BDD1B1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的双曲线C的右焦点为(2,0),右顶点为( ![]() ,0)
,0)
(1)求双曲线C的方程;
(2)若直线l:y=kx+ ![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 ![]() >2(其中O为原点).求k的取值范围.
>2(其中O为原点).求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=logax在区间(0,+∞)上是单调递增函数;命题q:不等式(a﹣2)x2+2(a﹣2)x﹣4<0对任意实数x恒成立.若p∨q为真命题,且p∧q为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com