
【题目】直线l过点M(2,1),且分别交x轴、y轴的正半轴于点A、B.点O是坐标原点.
(1)当△ABO的面积最小时,求直线l的方程;
(2)当![]()
![]() 最小时,求直线l的方程.
最小时,求直线l的方程.
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:

(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究,求至少有1人分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为实数,函数
为实数,函数![]() .
.
(1)求证: ![]() 不是
不是![]() 上的奇函数;
上的奇函数;
(2)若![]() 是
是![]() 上的单调函数,求实数
上的单调函数,求实数![]() 的值;
的值;
(3)若函数![]() 在区间
在区间![]() 上恰有3个不同的零点,求实数
上恰有3个不同的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A,B,C,D是直角坐标系中不同的四点,若![]() ,
,![]() ,且
,且![]() ,则下列说法正确的是( ),
,则下列说法正确的是( ),
A.C可能是线段AB的中点
B.D可能是线段AB的中点
C.C、D可能同时在线段AB上
D.C、D不可能同时在线段AB的延长线上
查看答案和解析>>
科目:高中数学 来源: 题型:
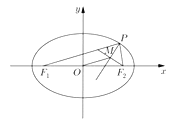
【题目】如图,点![]() 是双曲线
是双曲线![]()
![]() 上的动点,
上的动点,![]() 是双曲线的焦点,M是
是双曲线的焦点,M是![]() 的平分线上一点,且
的平分线上一点,且![]() ,某同学用以下方法研究
,某同学用以下方法研究![]() :延长
:延长![]() 交
交![]() 于点N,可知
于点N,可知![]() 为等腰三角形,且M为
为等腰三角形,且M为![]() 的中点,得
的中点,得![]() ,类似地:点
,类似地:点![]() 是椭圆
是椭圆![]()
![]() 上的动点,
上的动点,![]() 椭圆的焦点,M是
椭圆的焦点,M是![]() 的平分线上一点,且
的平分线上一点,且![]() 则
则![]() 的取值范围是______
的取值范围是______

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上的一个动点,且
上的一个动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 斜率为
斜率为![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 若存在,求
若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为P1,P2,则( )
A. P1P2=![]() B. P1=P2=
B. P1=P2=![]() C. P1+P2=
C. P1+P2=![]() D. P1<P2
D. P1<P2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,设直线
,设直线![]() ,其中
,其中![]() ,给出下列结论:
,给出下列结论:
①直线![]() 的方向向量与向量
的方向向量与向量![]() 共线;
共线;
②若![]() ,则直线
,则直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ;
;
③直线![]() 与直线
与直线![]() (
(![]() )一定平行;
)一定平行;
写出所有真命题的序号________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com